参数的假设检验

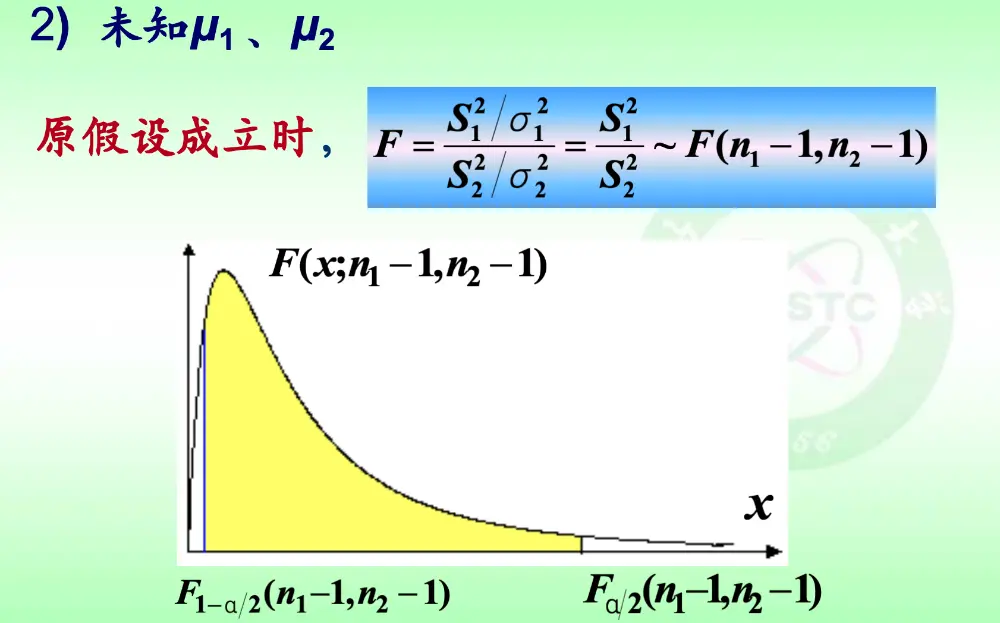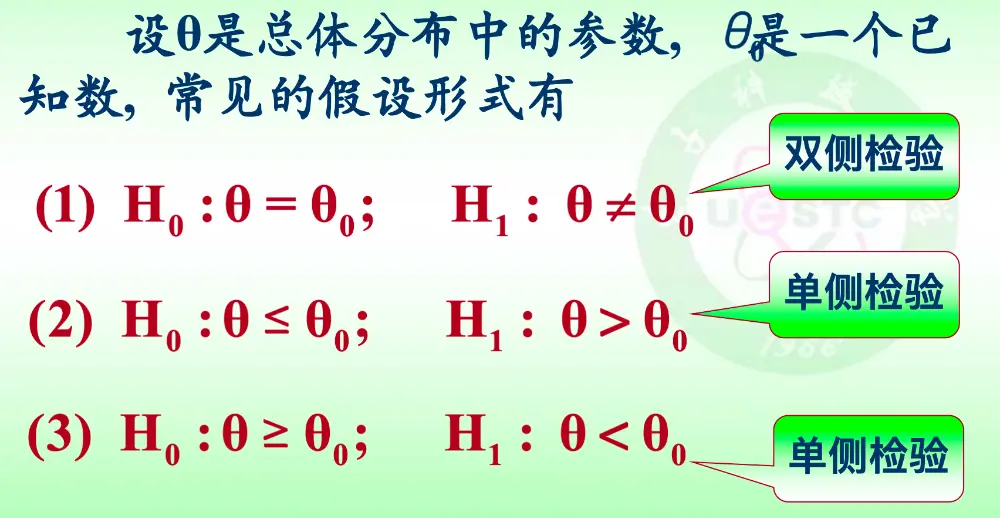
由于 ${\theta }_0$ 在单侧检验的时候不能确定代入，所以需要转化

---

正态总体均值检验

方差已知

方差未知

已知某产品的杂质含量服从正态分布 $N(\mu ,{\sigma }_2)$, 正常情况下杂质含量不超过 0.3%。某日抽检 16 批产品, 杂质含量值为 x1, x2, ··· , x16, 计算出 $\bar{x}$ = 0.43%, 样本标准差 s = 0.0032, 问: 这是一次偶然的杂质偏高, 还是产品品质出现了异常 ( 取显著性水平α= 0.05 ) ?

原假设不能文字描述

$$H_0:\mu \le 0.003$$ $$H_1:\mu >0.003$$

将 $H_0$ 调整为 $H_0:\mu =0.003$，未知方差，构造 t 分布假设统计量

$$\frac{\bar{X}-0.003}{s/\sqrt{n}}>t_{\alpha }(n-1)$$

这里拒绝域形式往往和对立假设形式相同

这两个假设不能反过来，当 $T$ 落在 $t_{1-\alpha }(n-1)$ 和 $t_{\alpha }(n-1)$ 中间的时候，两个都接受了，这时是因为导致假设不同推导的结论不同（这个是必然存在的，毕竟是信息不充分情况下的猜测）。我们倾向于在没有充分证据证明不正常的情况下都认为是系统误差的原因（偶然性原因），所以我们这么选择原假设

---

正态总体方差的检验

已知均值

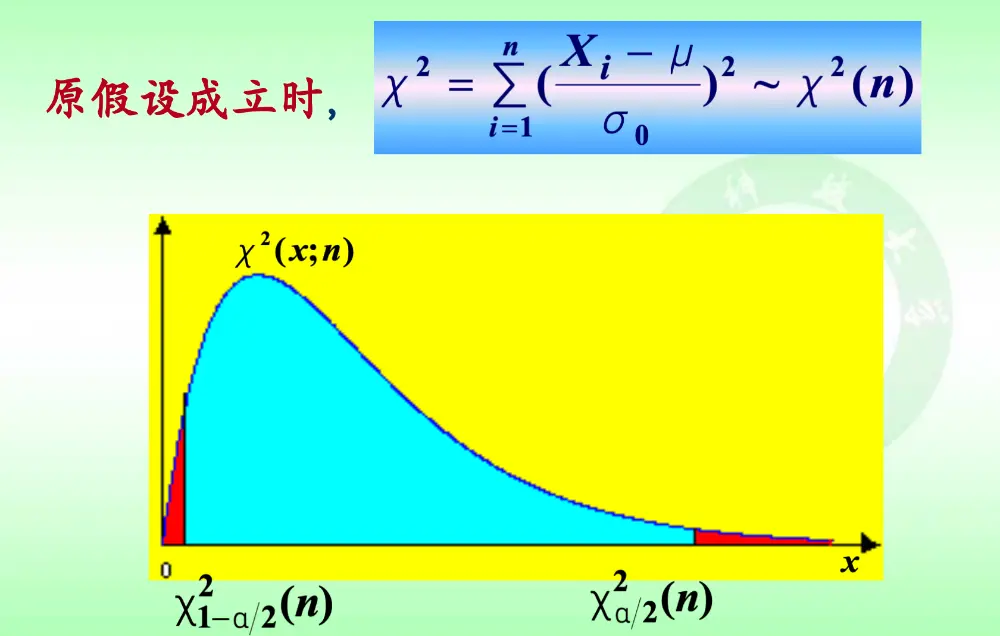
未知均值

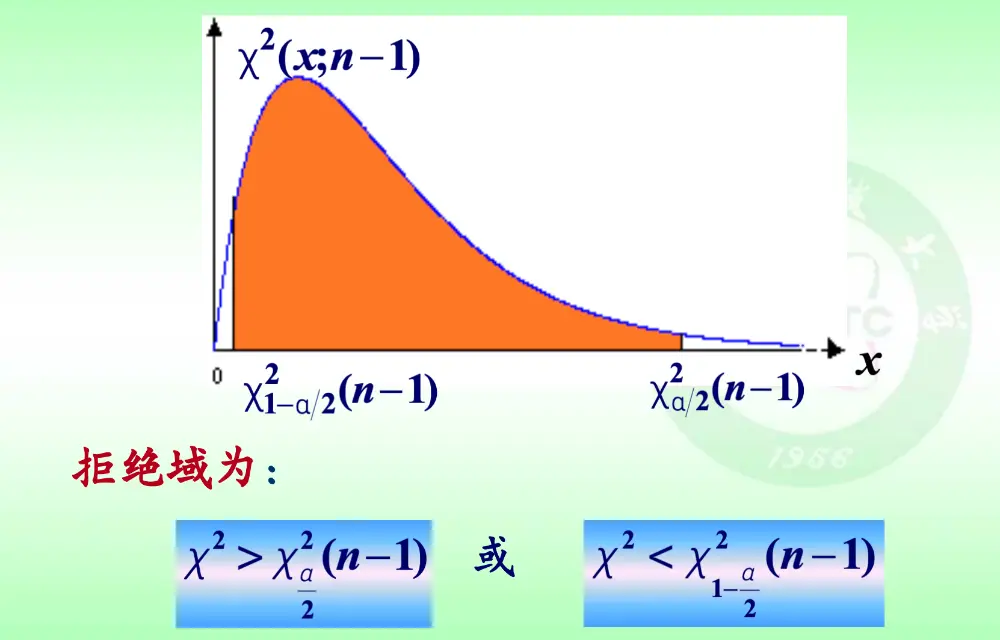
F 检验法