如果对于所有可能的输入序列,分别从状态 S1 和 S2 出发,所得到的输出和次态序列完全

对于完全确定状态
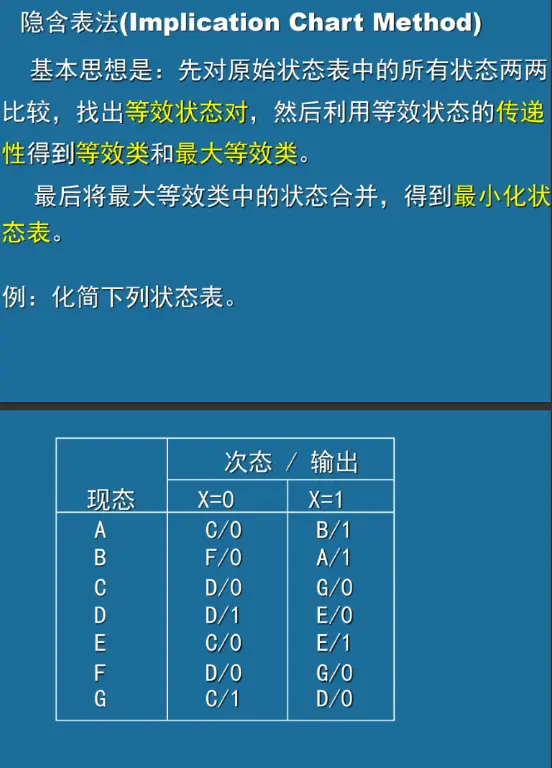
先将水平方向 A 与纵向的所有状态一一比较,再将 水平方向 B 与纵向一一比较,依此类推。 比较的结果有 3 种情况:
- 状态对等效 (在方格内填√)
- 如 DF
- 状态对不等效 (在方格内填×)
- 如 AD
- 状态对是否等效需要进一步检查 (填入次态对)
- 如 AB
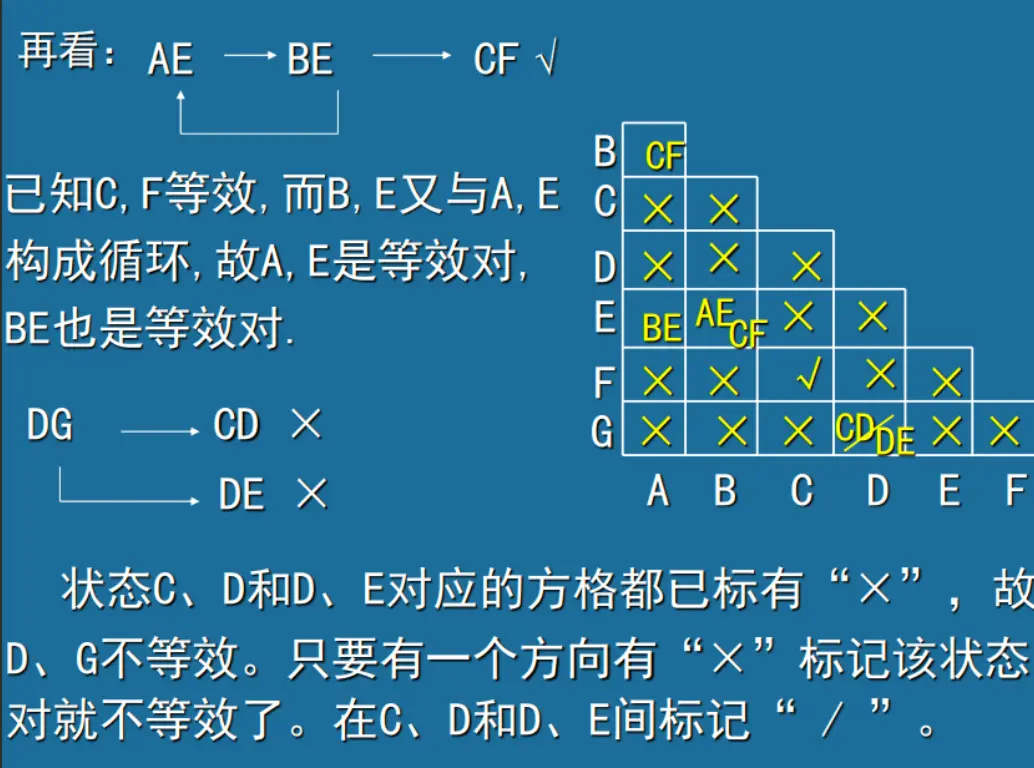
关联比较是要确定隐含表中待检查的那些次态对 是否等效。如果隐含表中某方格内有一个次态对不 等效,则该方格对应的两个状态就不等效。于是在 相应方格中增加标志“/ ” 。
若方格内的次态对均为等效状态对,则该方格对 应的状态为等效状态。该方格不增加任何标志。 例如:AB 对应的方格中次态为 CF,而 CF 有 “√” 表明 CF 等效,故判定 AB 等效
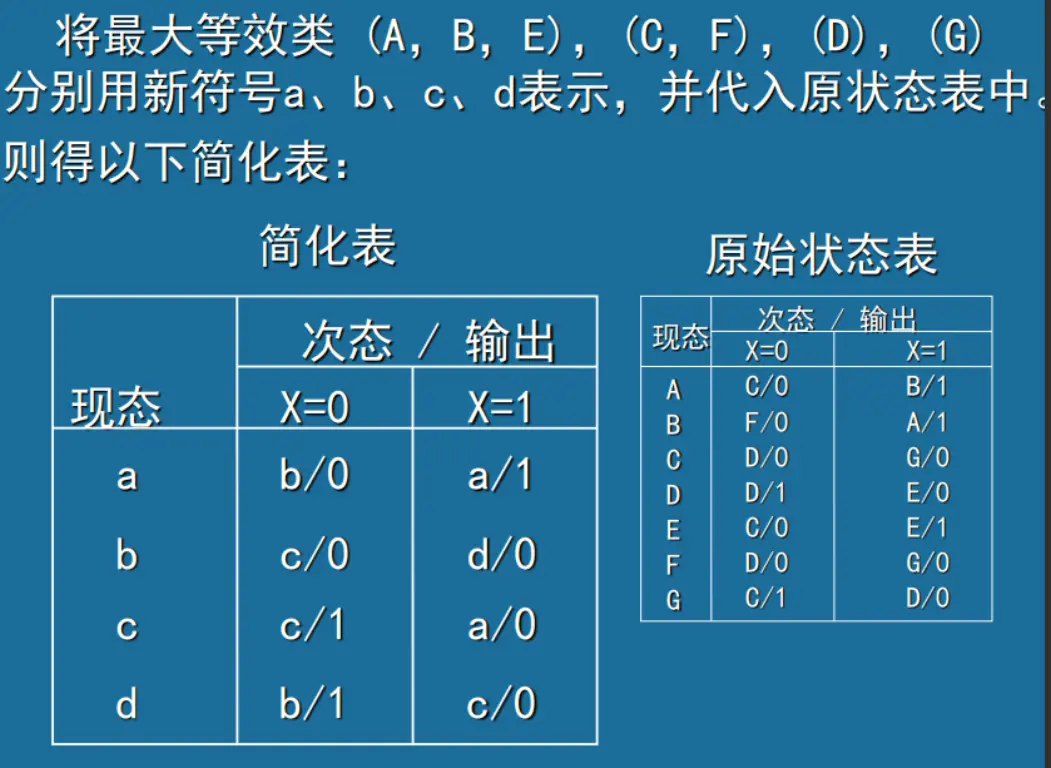
不完全确定状态
设 S1 和 S2 是不完全确定状态表中的两个状态,如果对于所有的有效输入序列,分别从 S1 和 S2 出发,所得到的输出响应序列和次态 (除不确定的那些位外) 是完全相同的,则 S1 和 S2 是相容的。或者说 S1 和 S2 是相容对,记为 (S1,S2),相容状态可以合并
相容状态没有传递性,为了从相容状态对中找出最大相容类,引入了状态合并图。它将状态以“点”的形式均匀的绘在圆周 上,然后把所有相容对都用线段连接起来,而所有点之间都有连线的多边型就构成了一个最大相容类(完全连边)
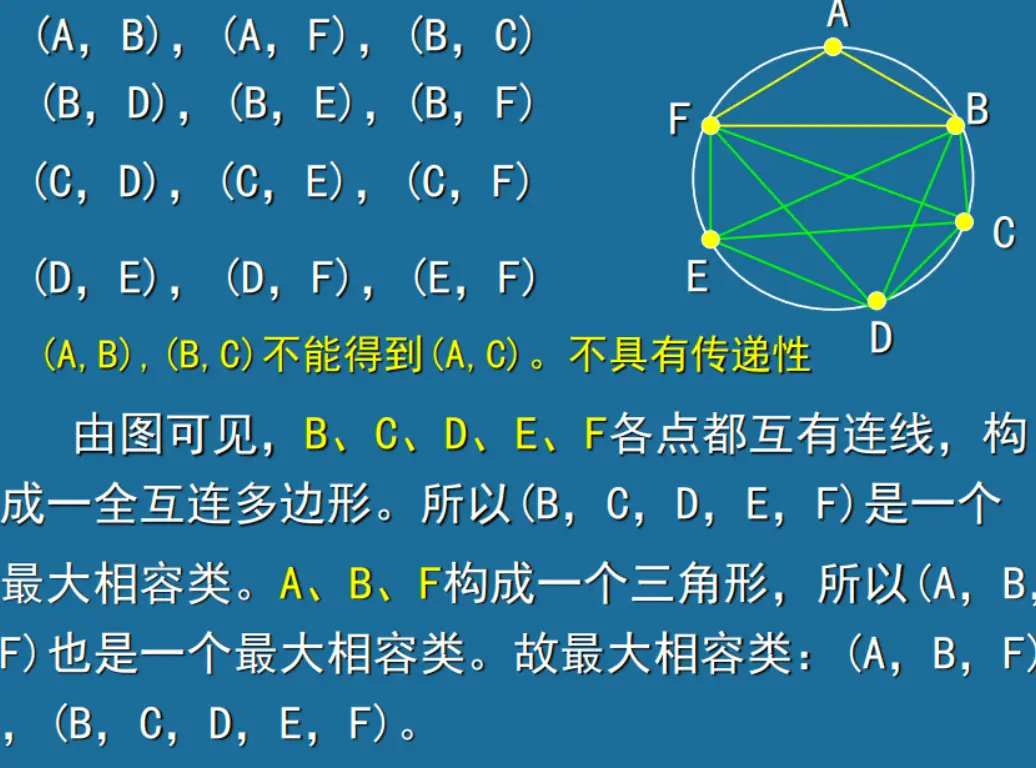
作最小化状态表时,先要从最大相容类中选出一组能覆盖原始状态表中全部状态的相容类,这一组 相容类必须满足以下三个条件
- 覆盖性。即所选的相容类的集合应包含原始状态表中的全部现态
- 最小性。即所选相容类集合中的相容类个数应最少
- 闭合性。即所选相容类集合中的任一相容类,在原始状态表中任一输入条件下产生的次态应该属于该集合中的某一相容类(不会跨相容类)
同时具备最小、闭合和覆盖三个条件的相容类的 (包含最大相容类) 集合,称最小闭覆盖。不完全确定状态表的最简化,就是寻找最小闭覆盖
