补码

补码又称“对 2 的补数”，补码表示法是: 如果数为正, 则正数的补码与原码表示形式相同. 如果数为负，则将负数的原码除符号位外，其余各位取反后末尾再加 1

[X]_{补}

时钟以 12 为计数循环，即以 12 为模。13 点在舍去模 12 后，即为 1 点。从 0 点出发，反时针拨 1 格即为－1 点，也可看成从 0 点顺时针拨 11 格，即 11 点。换句话说，在模 12 前提下，－1 可映射为＋11

确定模以后，我们将某数 X 对该模的补数称作其的补码。定义如下：

X_{补} = M + X

若 X>0，则模 M 作为正常的溢出量可以舍去。如同时钟一例舍去 12 一样

因而正数的补码就是其本身，形式与原码相同。（这个模是正数区域个数的两倍）

负数区域因为刚好加上正数区域的两倍，所以刚好落到正数的上面填满了整个定义域。

由此可以推出定点整数和定点小数的补码定义：

若二进制整数序列为: $\pm X_{n - 1} X_{n - 2} \dots X_{0}$ 则:

x_{原} = {X 2^{n + 1} - ∣ X ∣ 2^{n} > X \geq 0 0 \geq X > - 2^{n}

定点整数：

[x]_{补} = 2^{n} + x

定点小数：

[x]_{补} = 2 + x

也就是 2’s complement 名字的由来

若二进制小数序列为: $\pm 0. X_{- 1} X_{- 2} \dots X_{- n}$ 则:

x_{原} = {X 2 - ∣ X ∣ 2^{n} > X \geq 0 0 \geq X > - 2^{n}

由补码的一般表示式可看出：正数 X 的 X 补、X 反和 X 原是相同的

对于负数， X 补的符号位为 1，数值部分是将原码每位求反并尾数加 1。为什么呢？反码就是 $2^{n} - 1 - N$ ，在二进制上就像每个都取反了一样，而原码可以表示成 $(2^{n} - 1 - N) + 1$ 也就是在反码的基础上加一。

整数 0 的形式是唯一的。纯小数 0.0 的形式是唯一的。

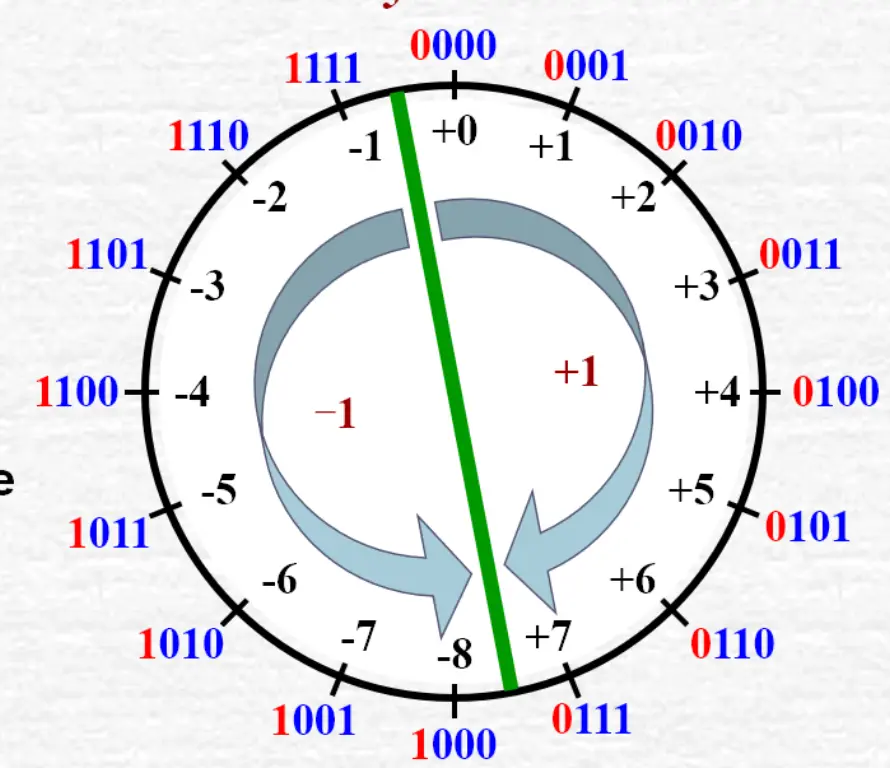
补码可能是自然的丢弃，也可能是异常的溢出行为

在模系统下，我们能够找到真值的对应是

- 2^{n - 1} \leq x \leq 2^{n - 1} - 1

小数点左移 n-1 位，则是小数补码形式

- 1 \leq x \leq 1 - 2^{- (n - 1)}

补码相当于最高位的权值是负的

🪴 Cyril