初步思路
通过边缘检测的算法能够将图像中的线条提取出来,每一个曲线对应的是无数条直线,只要找到一种方法统计在“同一条直线”上的小直线的数目,就能将图片中的“肉眼可见的直线”统计出来并在图上画出来
第一步提取边缘的曲线(无数小直线)的方法是在三个通道上去计算相邻像素的导数值,将这个区域的权重设置为导数值正相关的函数(可能要调整使得能够好分辨)。或着另一种思路是直接对图像二值化,然后直接通过相邻像素相减把边缘标记出来
第二步是将边缘的数据转化为很多条直线,也就是求等高线的切线,只要把梯度求出来做垂直就行了,代表的是这个图像的切线。
第三步是把直线的参数放在一起作为未知数放在坐标系里,这些点都代表着空间上一条唯一的线,那么某个区域的点越多,就说明有越多的“小直线”在同一条直线上。这个方法顺便也能把虚线这种断开的线给检测出来。如何判断这个区域有“很多点”呢?可以考虑区域分隔的统计方法
直线参数的研究
我们都知道斜率作为参数其范围是整个实数,当 k 很大或很小的时候,k 的大小就不能直观的反映出两个直线是不是一样斜了,b 也受 k 牵连,不是很好判断。所以考虑用与“旋转”概念最接近的极坐标表示直线的参数:
不难得出, 代表着直线到原点的距离,而 代表距离连线的倾斜角
下面考虑验证 和 对于随机取点形成的直线的随机分布:
对于在 的矩形区域内随机取两个点,记录其参数
x1 = rand(5000000,1);
y1 = rand(5000000,1);
x2 = rand(5000000,1);
y2 = rand(5000000,1);
% 根据方程计算得到 rho 和 theta
t=atan(-(x1-x2)./(y1-y2));
r=x1.*(cos(t))+y1.*(sin(t));
[histCount, histCenters] = hist3([t r], [70 70]);
surf(histCenters{:}, histCount)
colormap('hot')
colorbar
view(3)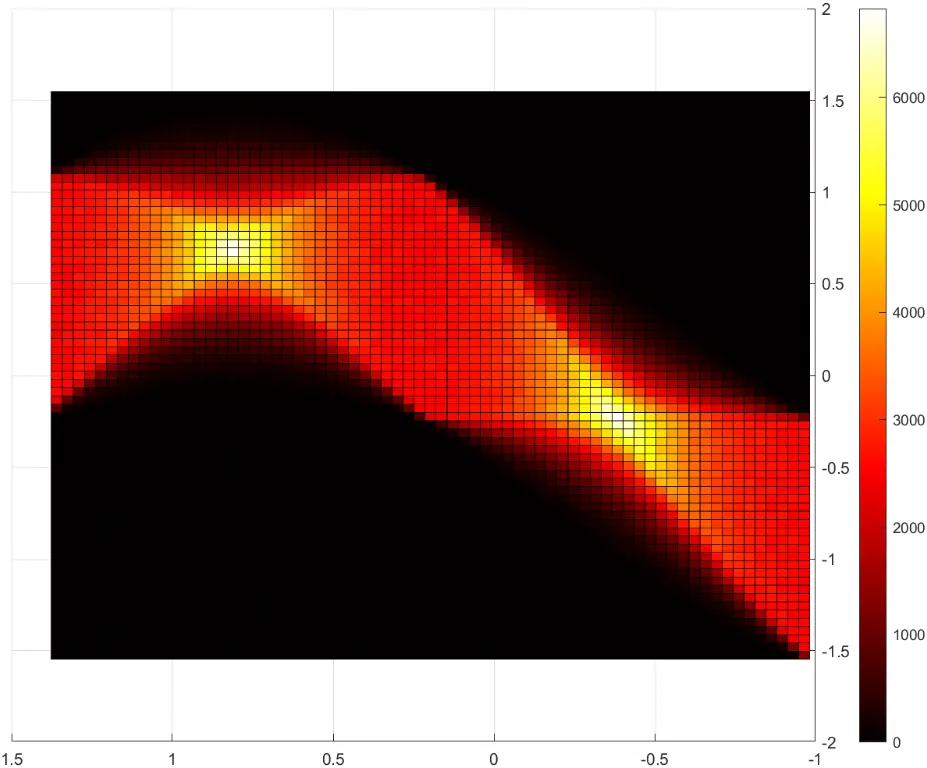
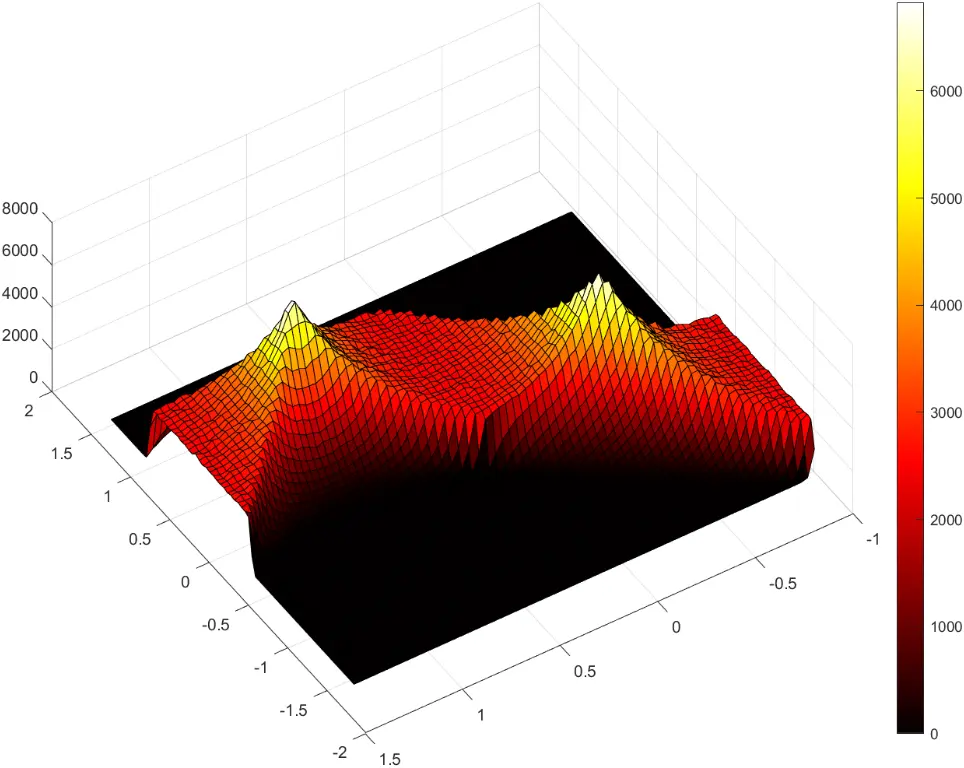
可以发现对于上面的方程,随机取点产生的参数 和 并不是在空间上呈现对称随机分布
推测是由于区域是正方形且取点都是正值造成的,考虑到图片一般为矩形,且在边缘出现直线的概率本身就是会比中心要少的特点,我们将原点移动到中心进行计算:
x1 = unifrnd(-1, 1, [5000000, 1]);
y1 = unifrnd(-1, 1, [5000000, 1]);
x2 = unifrnd(-1, 1, [5000000, 1]);
y2 = unifrnd(-1, 1, [5000000, 1]);
% 根据方程计算得到 rho 和 theta
t = atan(- (x1 - x2) ./ (y1 - y2));
r = x1 .* (cos(t)) + y1 .* (sin(t));
[histCount, histCenters] = hist3([t r], [70 70]);
surf(histCenters{:}, histCount)
colormap('hot')
colorbar
view(3)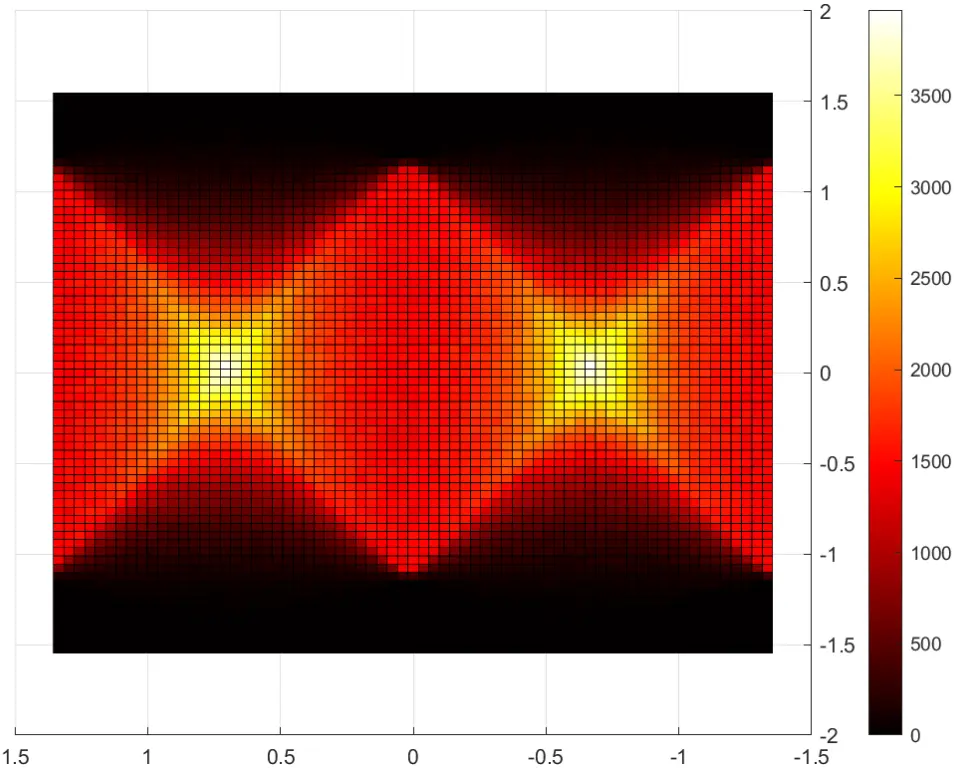
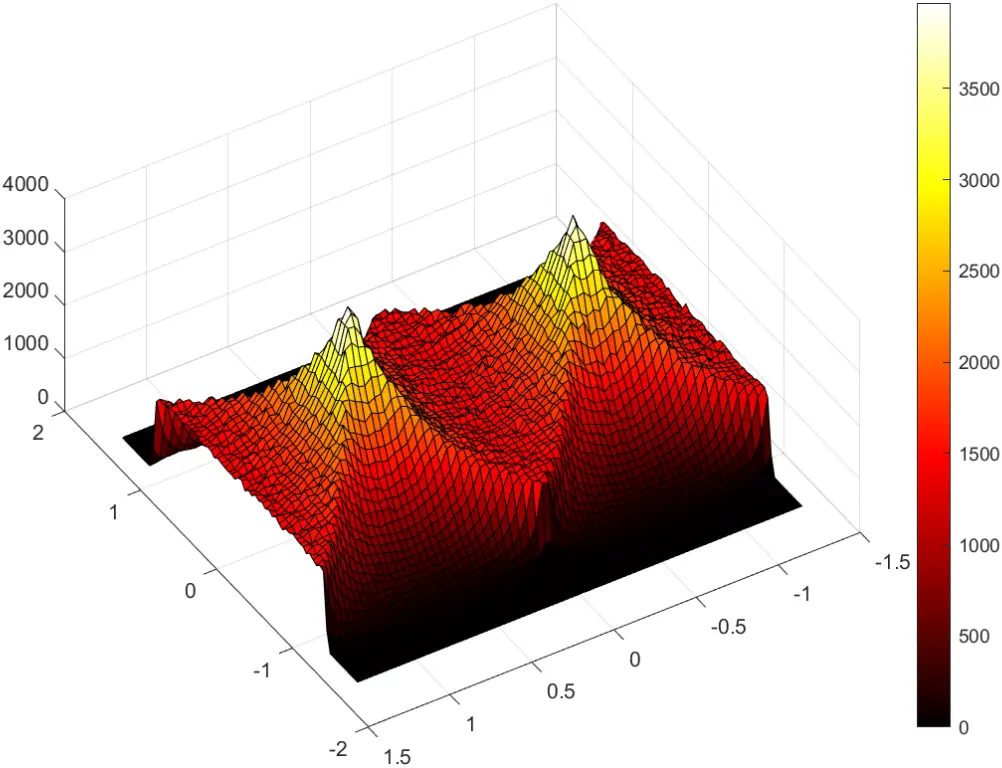
因为随机点生成的图像在对角线上的概率比其他的都要大,所以这个结果是合理的,同时也导致了在这个时候的距离会比较小(集中在原点了),其概率的集中是完全基于图像的、合理的,故考虑使用这个参数作为判断直线为同一条的判据。
图像处理
我们的目的是提取出图像的边缘,然后通过对边缘求切线得出每个位置的直线情况。同时根据边缘的明不明显可以设置一个权重,减少非边缘区域得出的没有意义的切线对统计结果的影响。这可以通过对图像求梯度实现,这样就能够同时得到边缘的方向信息和变化信息:
% 读取图像
img = imread('test.jpg');
% 转换为双精度
img = double(img);
% 分离三个通道
R = img(:,:,1);
G = img(:,:,2);
B = img(:,:,3);
% 计算每个通道的梯度
[GRx,GRy] = gradient(R);
[GGx,GGy] = gradient(G);
[GBx,GBy] = gradient(B);
成功得到图像的梯度
考虑到一个颜色渐变的图像,每个渐变点的梯度都很大,但是这个位置并不是一个突变的边缘,所以考虑计算二阶重偏导数
% 计算每个通道的二阶偏导数
del2R = del2(R);
del2G = del2(G);
del2B = del2(B);
可以看到突变的点大多数都明显的区分开了,这表明这个二阶重偏导数可以直接作为权重使用
参数方程的另外解释
前面的方法是提取切向量,对图像处理要求较高,如果在已知仅为边缘的一系列离散的点的情况,仍可以通过根据参数空间的特点求出“可能的直线”。
前面通过的是普通直角坐标系中一条线确定参数空间中的一个点,反过来,如果根据原来坐标系中的点,可以确定参数空间内的一条正弦曲线(参数用极坐标直线方程表示),这条线代表的是经过这个点的所有直线。而正弦曲线的交点就代表了原来坐标系内两个点形成的直线的参数。那么只要根据原来坐标系内的所有的点,画出所有的参数曲线,求出所有的交点,也就是每两个点连成的所有可能直线,再统计聚集的位置就能求出直线。
不过这个方法相当于遍历所有的点对(两个点),把很多相距很远、不相关的点也纳入考虑了,所以不是很好。
下面对这个方法进行测试:
% 测试直线 y = 3x - 2
x_values1 = -5:5;
y_values1 = 3 * x_values1 - 2;
% 添加噪声使得结果真实
y_values_noise1 = y_values1 + randn(1, size(x_values1, 2)) * 1.5;
% 测试直线 y = -2x + 1
x_values2 = -5:5;
y_values2 = -2 * x_values2 + 1;
% 添加噪声使得结果真实
y_values_noise2 = y_values2 + randn(1, size(x_values2, 2)) * 1.5;
hold on
% 设置角度范围
theta_values = -pi / 2:0.01:pi / 2;
for i = 1:size(x_values1, 2)
rho_values1 = y_values_noise1(i) * sin(theta_values) + x_values1(i) * cos(theta_values);
plot(theta_values, rho_values1);
end
for i = 1:size(x_values2, 2)
rho_values2 = y_values_noise2(i) * sin(theta_values) + x_values2(i) * cos(theta_values);
plot(theta_values, rho_values2);
end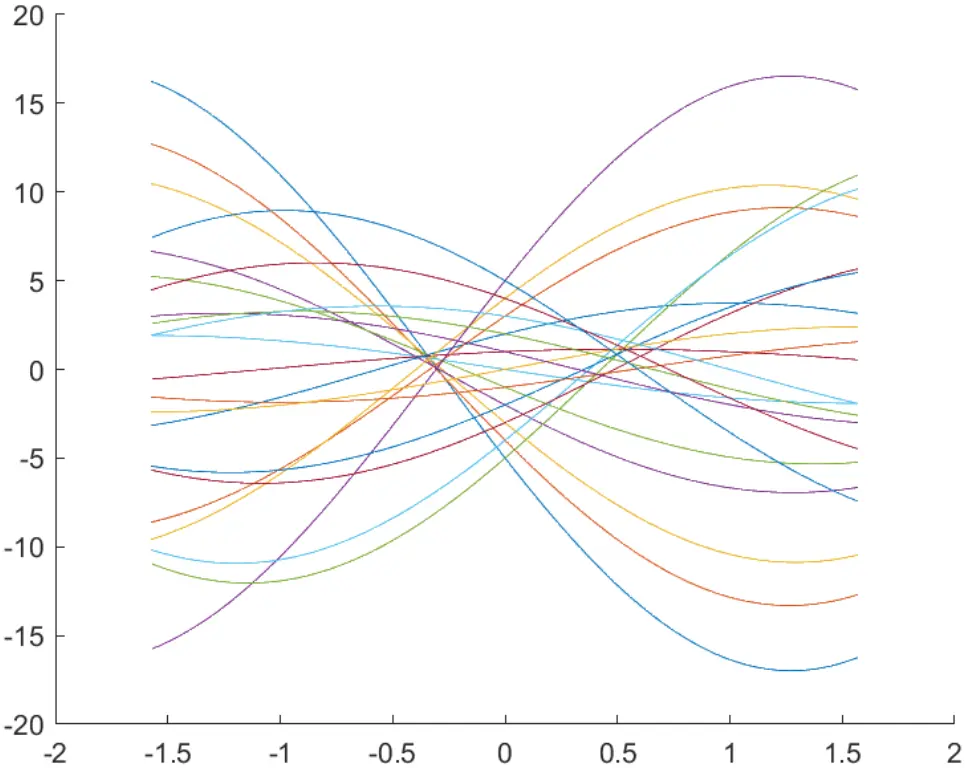
可以看出这里有两个聚集点,分别对应两个直线;而在两个聚集点外仍有很多交点,这些交点代表的是不是同一个边缘的点连成的直线的参数,所以是多余的。故下面采用最前面提到的方法
对图像的直线检测实现
首先计算图片的梯度和二阶导,根据梯度求出 和 ,根据二阶导的权重放入统计中,做出热力图。
clear;
% 读取图像
img = imread('1.jpg');
% 转换为双精度
img = double(img);
% 分离三个通道
R = img(:, :, 1);
G = img(:, :, 2);
B = img(:, :, 3);
% debug
% R = double([0, 0, 0, 0; 0, 0, 0, 0; 128, 128, 128, 128; 0, 0, 0, 0; 0, 0, 0, 0]);
% G = double([0, 0, 0, 0; 0, 0, 0, 0; 128, 128, 128, 128; 0, 0, 0, 0; 0, 0, 0, 0]);
% B = double([0, 0, 0, 0; 0, 0, 0, 0; 128, 128, 128, 128; 0, 0, 0, 0; 0, 0, 0, 0]);
% 计算每个通道的梯度
[GBx, GBy] = gradient(B);
[GGx, GGy] = gradient(G);
[GRx, GRy] = gradient(R);
% 取绝对值
GBx = abs(GBx); GBy = abs(GBy);
GGx = abs(GGx); GGy = abs(GGy);
GRx = abs(GRx); GRy = abs(GRy);
% 计算每个通道的二阶偏导数
[GRxx, GRxy] = gradient(GRx);
[GRyx, GRyy] = gradient(GRy);
[GGxx, GGxy] = gradient(GGx);
[GGyx, GGyy] = gradient(GGy);
[GBxx, GBxy] = gradient(GBx);
[GByx, GByy] = gradient(GBy);
% 取绝对值
GRxx = abs(GRxx); GRxy = abs(GRxy);
GRyx = abs(GRyx); GRyy = abs(GRyy);
GGxx = abs(GGxx); GGxy = abs(GGxy);
GGyx = abs(GGyx); GGyy = abs(GGyy);
GBxx = abs(GBxx); GBxy = abs(GBxy);
GByx = abs(GByx); GByy = abs(GByy);
% 转化为方向导数的长度
del2R = sqrt(GRxx .^ 2 + GRyy .^ 2);
del2G = sqrt(GGxx .^ 2 + GGyy .^ 2);
del2B = sqrt(GBxx .^ 2 + GByy .^ 2);
% 根据梯度求出 $\theta$ 和 $\rho$
thetaR = atan2(GRy, -GRx);
thetaG = atan2(GGy, -GGx);
thetaB = atan2(GBy, -GBx);
% $\rho=x\cos\theta+y \sin\theta$ x,y是原点为图片中心的坐标
y = (size(R, 1):-1:1) - ones(1, size(R, 1)) .* round(size(R, 1) / 2);
x = (1:size(R, 2)) - ones(1, size(R, 2)) .* round(size(R, 2) / 2);
[X, Y] = meshgrid(x, y);
X = reshape(X, 1, []);
Y = reshape(Y, 1, []);
thetaR = reshape(thetaR, 1, []);
thetaG = reshape(thetaG, 1, []);
thetaB = reshape(thetaB, 1, []);
del2R = reshape(del2R, 1, []);
del2G = reshape(del2G, 1, []);
del2B = reshape(del2B, 1, []);
rhoR = X .* cos(thetaR) + Y .* sin(thetaR); % bug fix
rhoG = X .* cos(thetaG) + Y .* sin(thetaG);
rhoB = X .* cos(thetaB) + Y .* sin(thetaB);
% 以二阶导数为权重,拼接通道的统计值,并显示热力图,将 rho 和 theta 转换为一维数组
rho = [rhoR, rhoG, rhoB];
theta = [thetaR, thetaG, thetaB];
del2_all = [del2R, del2G, del2B];
% 计算二维直方图
% 以 rho 为 x 轴,theta 为 y 轴,del2 为权重
rho_edges = linspace(min(rho(:)), max(rho(:)), 31);
theta_edges = linspace(min(theta(:)), max(theta(:)), 31);
% 将 rho 和 theta 转换为直方图的 bin 索引
[~, ~, rho_idx] = histcounts(rho, rho_edges);
[~, ~, theta_idx] = histcounts(theta, theta_edges);
% 计算加权的直方图
weighted_hist = accumarray([rho_idx(:), theta_idx(:)], del2_all(:), [length(rho_edges) - 1, length(theta_edges) - 1]);
% 显示加权的直方图
figure;
% imagesc(rho_edges(1:end-1), theta_edges(1:end-1), weighted_hist);
scatter(rho, theta, 10, del2_all, 'filled');
xlabel('\rho');
ylabel('\theta');但是实验的结果并不理想。使用二阶导作为权重会导致统计的梯度不在边缘地区而是有偏移,而且默认的梯度为 0,导致结果中有很多垃圾数据。而这一切的原因都是我们使用的是二阶导来判断边缘
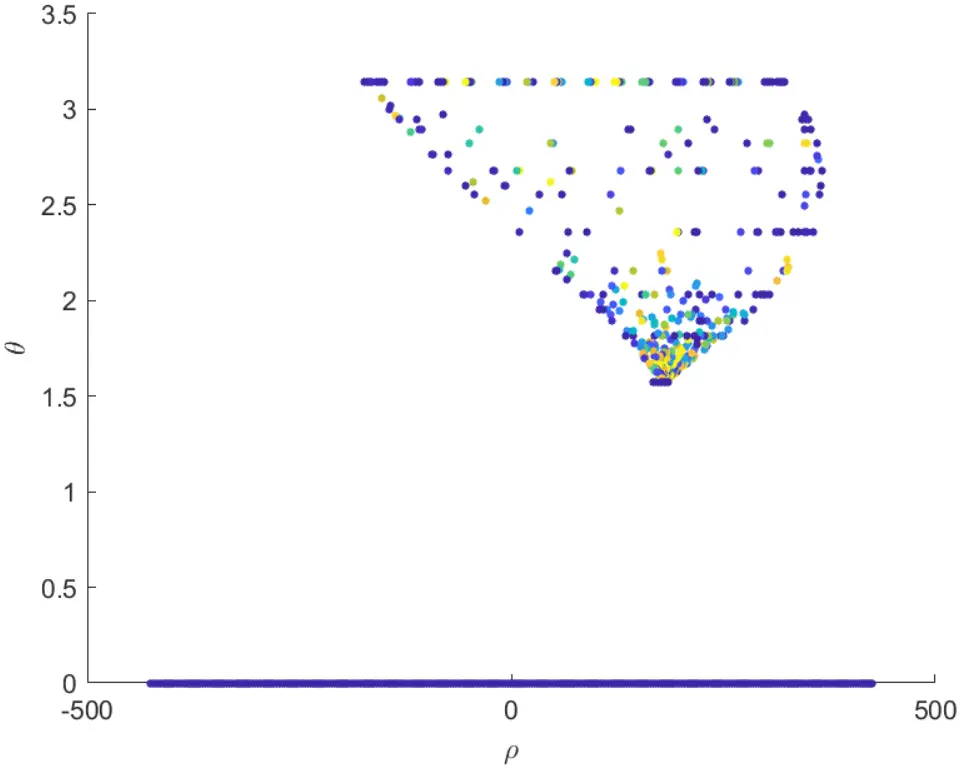
故考虑使用其他方法判断边缘
Canny 边缘检测算法
canny 边缘检测算法分为 5 个步骤:
- 对图像的噪声进行抑制
- 就是对图像进行平滑操作,其实就是高斯模糊
- 计算图像的梯度和方向
- 用差分算法,和上边一样,对八个方向相邻像素分析
- 非极大值抑制
- 当梯度达到局部的最大值的时候,我们就认为它是图像的边缘
- 而对于非极大值的点,即使超过了我们设定的“边缘梯度阈值”,也不认为它是边缘
- 实现具体操作:
- 沿着梯度的方向判断就可以了
- 双阈值检测
- 定义两种阈值,分成不是边缘、弱边缘、强边缘三种
- 边缘连接
- 不和强边缘连接的弱边缘就归零
- 否则升为强边缘
function [edges, grad_x, grad_y, theta] = canny(img)
img = double(img);
gauss = [1, 2, 1; 2, 4, 2; 1, 2, 1] / 16; % 3*3高斯滤波器
sobel_x = [-1, 0, 1; -2, 0, 2; -1, 0, 1]; % Sobel水平算子
sobel_y = [-1, -2, -1; 0, 0, 0; 1, 2, 1]; % Sobel垂直算子
img = conv2(img, gauss, 'same'); % 高斯滤波
grad_x = conv2(img, sobel_x, 'same'); % Sobel水平边缘检测
grad_y = conv2(img, sobel_y, 'same'); % Sobel垂直边缘检测
M = sqrt(grad_x .^ 2 + grad_y .^ 2); % 边缘的梯度幅值
theta = atan2(grad_y, grad_x); % 边缘的梯度方向
% 如果小于0,加上pi
theta(theta < 0) = theta(theta < 0) + pi;
N = zeros(size(M)); % 非极大值抑制后的图像
% 非极大值抑制
for i = 2:length(M(:, 1)) - 1
for j = 2:length(M(1, :)) - 1
dirc = theta(i, j);
if abs(dirc) <= pi / 8
if M(i, j) == max([(M(i, j - 1)), M(i, j), M(i, j + 1)])
N(i, j) = M(i, j);
end
elseif abs(dirc) >= 3 * pi / 8
if M(i, j) == max([(M(i - 1, j)), M(i, j), M(i + 1, j)])
N(i, j) = M(i, j);
end
elseif dirc > pi / 8 && dirc < 3 * pi / 8
if M(i, j) == max([(M(i - 1, j - 1)), M(i, j), M(i + 1, j + 1)])
N(i, j) = M(i, j);
end
elseif dirc > (- 3) * pi / 8 && dirc < (- pi) / 8
if M(i, j) == max([(M(i + 1, j - 1)), M(i, j), M(i - 1, j + 1)])
N(i, j) = M(i, j);
end
end
end
end
% 双阈值检测
th = 0.4 * max(N(:));
tl = 0.2 * max(N(:));
th_edge = N > th;
tl_edge = N > tl;
% 连接边缘
% 边拓展
th_edge = padarray(th_edge, [1, 1], 0, 'both');
tl_edge = padarray(tl_edge, [1, 1], 0, 'both');
vised = zeros(size(th_edge));
% 初始化输出图像
edge_connected = false(size(tl_edge));
% 找到所有高阈值边缘像素
[rows, cols] = find(th_edge);
% 对于每一个高阈值边缘像素
for k = 1:length(rows)
% 使用深度优先搜索连接边缘
stack = [rows(k), cols(k)]; % 初始化栈
while ~isempty(stack)
% pop
r = stack(1, 1);
c = stack(1, 2);
stack(1, :) = [];
if vised(r, c)
continue;
end
% 标记这个像素为已访问
vised(r, c) = true;
% 如果这个像素是一个低阈值边缘像素,就把它添加到输出图像中
if tl_edge(r, c)
edge_connected(r, c) = true;
% 把这个像素的所有邻居添加到栈中
for dr = -1:1
for dc = -1:1
if dr ~= 0 || dc ~= 0
r2 = r + dr;
c2 = c + dc;
if r2 >= 1 && r2 <= size(tl_edge, 1) && c2 >= 1 && c2 <= size(tl_edge, 2)
stack = [stack; r2, c2];
end
end
end
end
end
end
end
edges = edge_connected(2:end - 1, 2:end - 1);
end
hough 变换验证可行性
替换上面的方法为 canny 检测,只统计边缘的点
clear;
% 读取图像
img = imread('1.png');
% 转换为双精度
img = double(img);
% 分离三个通道
R = img(:, :, 1);
G = img(:, :, 2);
B = img(:, :, 3);
% % debug
% R = double([0, 0, 0, 0; 0, 0, 0, 0; 128, 128, 128, 128; 0, 0, 0, 0; 0, 0, 0, 0]);
% G = double([0, 0, 0, 0; 0, 0, 0, 0; 128, 128, 128, 128; 0, 0, 0, 0; 0, 0, 0, 0]);
% B = double([0, 0, 0, 0; 0, 0, 0, 0; 128, 128, 128, 128; 0, 0, 0, 0; 0, 0, 0, 0]);
% 用canny计算边缘和梯度信息
[edgesR, grad_xR, grad_yR, thetaR] = canny(R);
[edgesG, grad_xG, grad_yG, thetaG] = canny(G);
[edgesB, grad_xB, grad_yB, thetaB] = canny(B);
% $\rho=x\cos\theta+y \sin\theta$ x,y是原点为图片中心的坐标
y = (size(R, 1):-1:1) - ones(1, size(R, 1)) .* round(size(R, 1) / 2);
x = (1:size(R, 2)) - ones(1, size(R, 2)) .* round(size(R, 2) / 2);
[X, Y] = meshgrid(x, y);
X = reshape(X, 1, []);
Y = reshape(Y, 1, []);
thetaR = reshape(thetaR, 1, []);
thetaG = reshape(thetaG, 1, []);
thetaB = reshape(thetaB, 1, []);
% 删除非边缘像素
counter = 1;
for i = 1:size(X, 2)
if edgesR(i) == 1 || edgesG(i) == 1 || edgesB(i) == 1
new_x(counter) = X(i);
new_y(counter) = Y(i);
thetaR(counter) = thetaR(i);
thetaG(counter) = thetaG(i);
thetaB(counter) = thetaB(i);
counter = counter + 1;
end
end
thetaR(counter:end) = [];
thetaG(counter:end) = [];
thetaB(counter:end) = [];
rhoR = new_x .* cos(thetaR) + new_y .* sin(thetaR);
rhoG = new_x .* cos(thetaG) + new_y .* sin(thetaG);
rhoB = new_x .* cos(thetaB) + new_y .* sin(thetaB);
rho = [rhoR, rhoG, rhoB];
theta = [thetaR, thetaG, thetaB];
% 计算热力图
figure
hist3([rho', theta'], [50, 50], 'CDataMode', 'auto'); % 添加颜色
xlabel('\rho');
ylabel('\theta');
title('Hough Transform');
colormap('hot'); % 使用热色图
colorbar; % 添加颜色条
grid on; % 开启网格
view(3); % 改变视角为3D视图
shading interp; % 平滑颜色过渡
lighting phong; % 添加光照效果
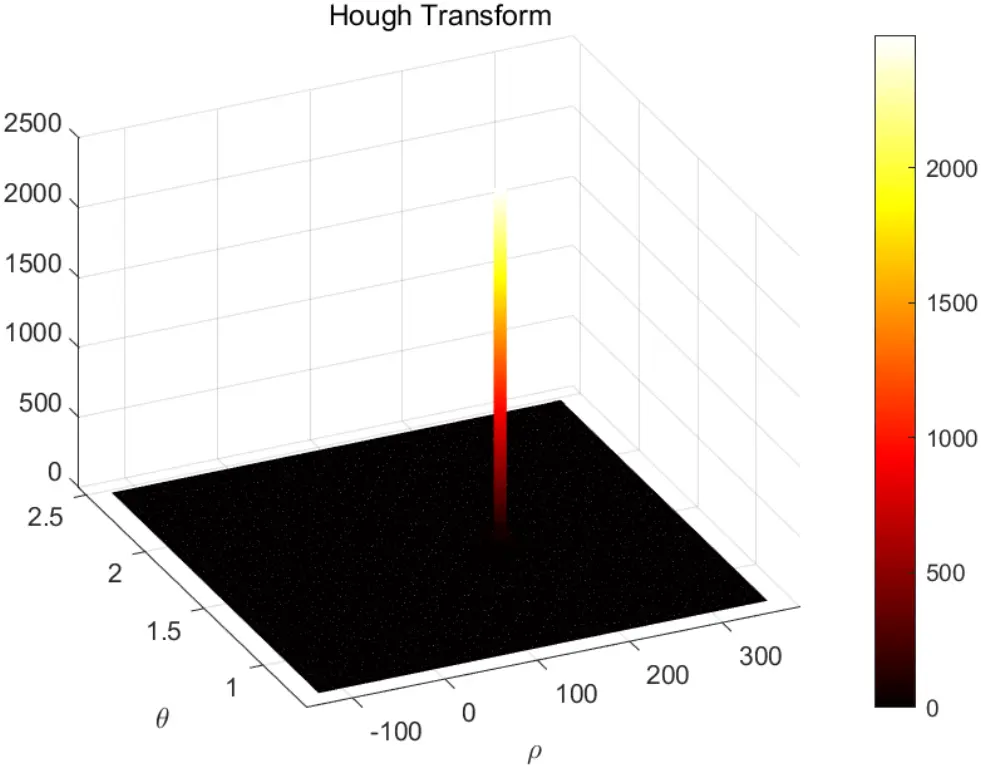


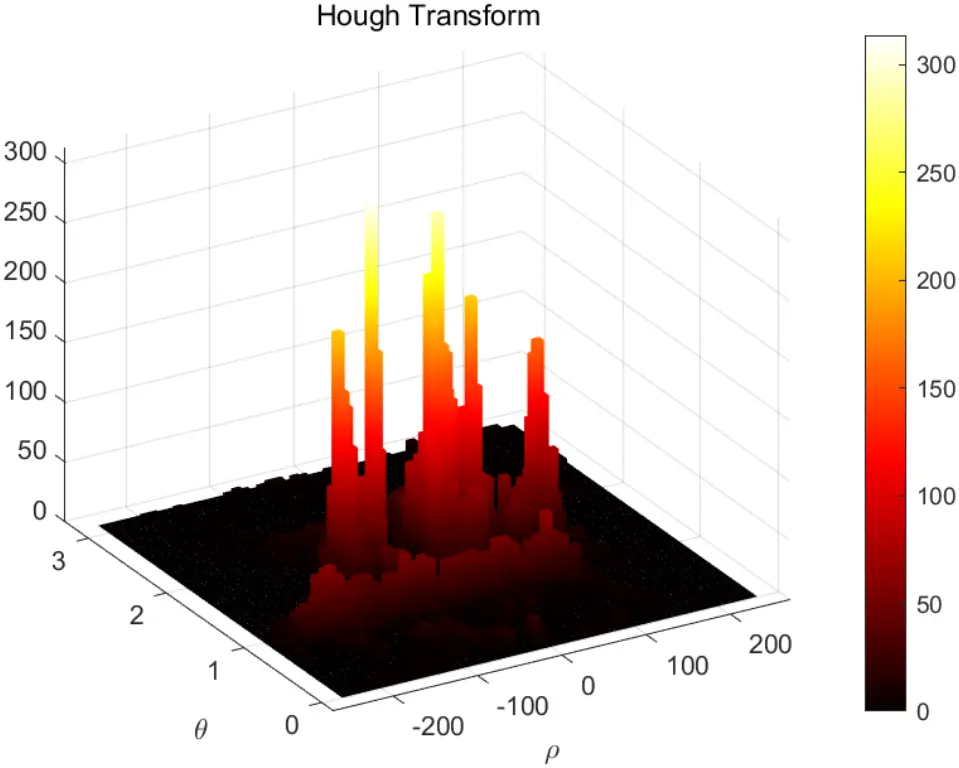
初步验证了可行性
对图像进行映射
进过实际操作,考虑到映射到原图上的难度,一开始的原点还是定在左下角了
...
y = 1:size(R, 1);
x = 1:size(R, 2);
...
% 计算直方图并找到高度大于0.3的bins
[N, edgesRho, edgesTheta] = histcounts2(rho, theta, [50, 50]);
% 设定一个阈值200
[idx_row, idx_col] = find(N > 200);
% 计算直线的两个端点并绘制直线
figure
img = imread('2.png');
imshow(img); % 重新读取图像
hold on;
for i = 1:length(idx_row)
rhoMax = (edgesRho(idx_row(i)) + edgesRho(idx_row(i) + 1)) / 2;
thetaMax = (edgesTheta(idx_col(i)) + edgesTheta(idx_col(i) + 1)) / 2;
x = [0, size(X, 2)];
y = (rhoMax - x * cos(thetaMax)) / sin(thetaMax);
plot(x, y, 'r', 'LineWidth', 2);
end
hold off;最终效果


未解决的问题
求出来的直线是跨越整个图像的,如何求出特定的线段呢?