FP tree 算法可以优化
https://wizardforcel.gitbooks.io/dm-algo-top10/content/apriori.html
找到频繁 k 项集的代码放在附件里


实验内容简介
本实验旨在实现并验证频繁模式挖掘算法中的 Apriori 算法,主要任务是通过设定最小支持度和置信度参数,从数据集中挖掘频繁项集和关联规则。频繁模式挖掘是一种在大数据集或事务数据库中发现常见模式的技术。它被广泛应用于市场篮子分析、推荐系统和其他关联规则挖掘的领域。
算法说明
算法概述
Apriori 算法通过逐层生成频繁项集,筛选出满足最小支持度的项集,然后基于这些频繁项集生成关联规则。
- 支持度 (Support):项集在事务数据库中出现的频率,支持度值越高,说明该项集越常见。设定的最小支持度是为了筛选出频繁出现的项集。
- 置信度 (Confidence):表示规则的可靠性,置信度越高,说明规则更可信。置信度用于衡量在频繁项集中挖掘的规则是否具有实际意义。
核心函数:
get_item_set_tran_list:从输入文件中读取事务数据,将其转换为项集列表和事务列表,为后续挖掘做准备。itemset_with_min_support:通过支持度过滤项集,保留满足最小支持度的项集。join_set:将不同频繁项集组合为更大项集,以便进行进一步的支持度检测。generate_subsets和get_subsets:用于生成项集的所有非空子集,为关联规则生成提供支持。run_apriori:主要算法执行函数,调用各个子函数完成频繁项集的挖掘,并生成满足最小置信度的关联规则。
算法分析与设计
数据结构设计
- 使用
ItemSet表示单个项集,ItemSetList表示多个项集组成的事务列表。 - 使用
ItemSetSet表示频繁项集集合,ItemSetCount表示项集及其出现次数,用于快速查找项集的支持度。
流程设计
- 数据预处理:从 CSV 文件中读取数据,将每行转换为项集。
- 频繁项集生成:首先生成单个项的频繁项集,随后逐步生成更大项集。
- 例如,生成频繁二项集时,会将单项集进行组合,形成候选二项集,再通过支持度筛选。
- 关联规则生成:对于每个频繁项集的非空子集,计算置信度,满足最小置信度的子集则作为关联规则。
剪枝过程
在生成候选项集时,对不满足支持度的项集直接剔除,以减少计算量。
代码实现细节
run_apriori函数调用itemset_with_min_support和join_set,根据支持度进行剪枝,并逐层生成频繁项集。print_result函数用于格式化输出频繁项集和关联规则,方便分析。
测试结果
实验数据
使用名为“INTEGRATED-DATASET.csv”的数据集,该数据集包含多个事务,每个事务包含若干项。每一行代表一个事务,项之间用逗号分隔。
结果展示
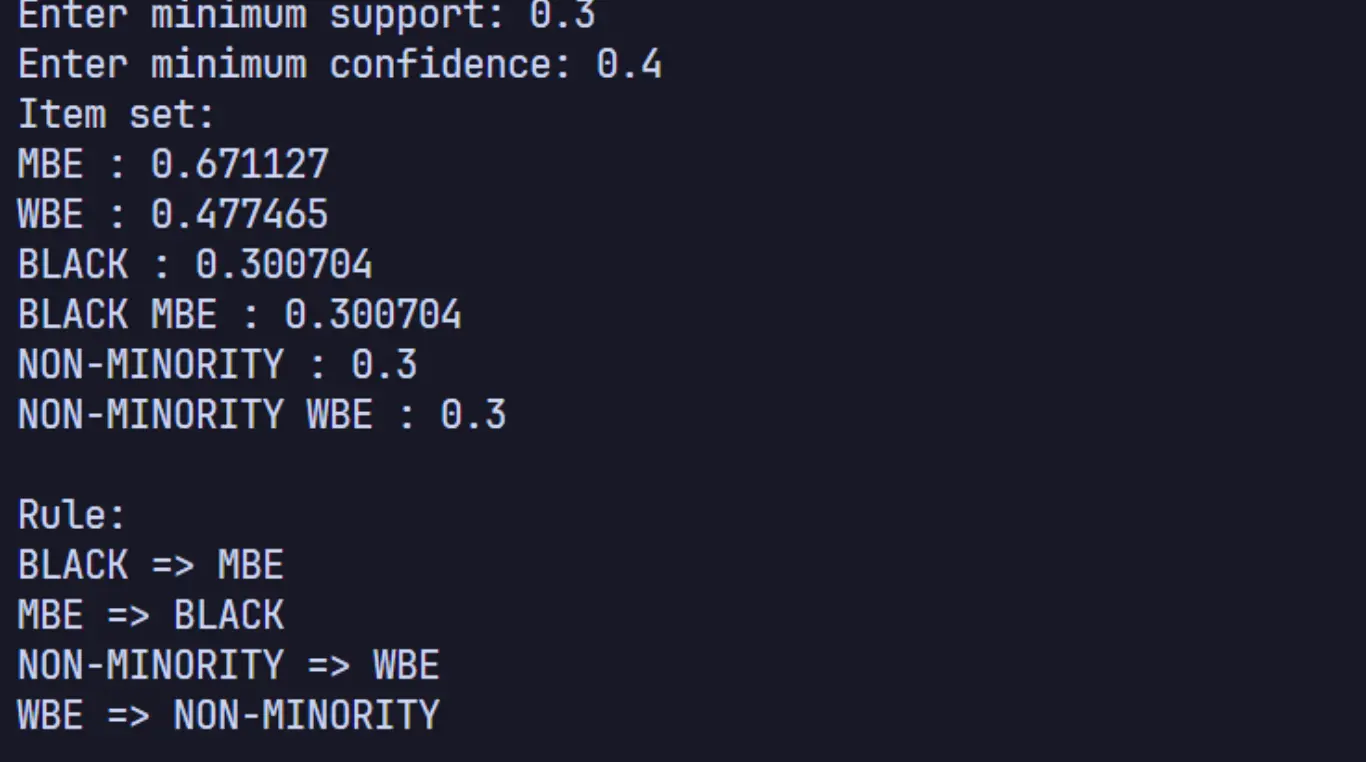
分析与探讨
算法效率分析
Apriori 算法在小规模数据集上效果较好,但在大规模数据集上会由于候选项集的生成而产生较大的计算开销,可能导致性能瓶颈。
局限性
Apriori 算法需要多次扫描数据集,每次扫描都会生成候选项集,导致在稀疏数据集上效率较低。
附录:源代码
#include <algorithm>
#include <fstream>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <string>
#include <vector>
using namespace std;
typedef set<string> ItemSet;
typedef vector<ItemSet> ItemSetList;
typedef map<string, int> ItemCount;
typedef map<ItemSet, int> ItemSetCount;
typedef set<ItemSet> ItemSetSet;
typedef map<ItemSet, ItemSet> AprioriRule;
struct AprioriResult {
map<ItemSet, double> itemsWithSupport;
AprioriRule rule;
};
struct ItemSetTransactionList {
ItemSetSet item_set_set;
ItemSetList transaction_list;
};
ItemSetTransactionList get_item_set_tran_list(const string file) {
ifstream fin(file);
string line;
ItemSetTransactionList item_set_tran_list;
while (getline(fin, line)) {
size_t pos_begin = 0;
ItemSet line_item_set;
while (pos_begin < line.size()) {
size_t pos_end = line.find(',', pos_begin);
if (pos_end == string::npos) {
pos_end = line.size();
}
string item = line.substr(pos_begin, pos_end - pos_begin);
item_set_tran_list.item_set_set.insert(ItemSet{item});
line_item_set.insert(item);
pos_begin = pos_end + 1;
}
item_set_tran_list.transaction_list.push_back(line_item_set);
}
return item_set_tran_list;
}
/**
* @brief Get the itemset with minimum support
*
* @param item_count 每个item的出现次数
* @return 在 transaction_list 中出现次数大于minS的 item_set_set 的子集
*/
ItemSetSet itemset_with_min_support(const ItemSetList &transaction_list,
const ItemSetSet &item_set_set,
const double minS,
ItemSetCount &items_count) {
ItemSetSet local_set = {};
ItemSetCount local_items_count;
for (ItemSet items : item_set_set) {
for (ItemSet trans_item_set : transaction_list) {
if (includes(trans_item_set.begin(), trans_item_set.end(),
items.begin(), items.end())) {
items_count[items]++;
local_items_count[items]++;
}
}
}
for (auto count : local_items_count) {
if ((double)count.second / (double)transaction_list.size() >= minS) {
local_set.insert(count.first);
}
}
return local_set;
}
ItemSetSet join_set(const ItemSetSet &item_set_set, size_t k) {
ItemSetSet join_set;
for (ItemSet item_set1 : item_set_set) {
for (ItemSet item_set2 : item_set_set) {
if (item_set1.size() == item_set2.size()) {
ItemSet new_item_set = item_set1;
new_item_set.insert(item_set2.begin(), item_set2.end());
if (new_item_set.size() == k) {
join_set.insert(new_item_set);
}
}
}
}
return join_set;
}
void generate_subsets(ItemSet &item_set, ItemSet ¤t, int index,
ItemSetSet &result) {
if (!current.empty()) {
result.insert(current);
}
for (size_t i = index; i < item_set.size(); i++) {
auto it = next(item_set.begin(), i);
current.insert(*it);
generate_subsets(item_set, current, i + 1, result);
current.erase(*it);
}
}
ItemSetSet get_subsets(ItemSet item_set) {
ItemSetSet result;
ItemSet current;
generate_subsets(item_set, current, 0, result);
return result;
}
AprioriResult run_apriori(string file, const double minS, const double minC) {
ItemSetTransactionList item_set_tran_list = get_item_set_tran_list(file);
ItemSetSet item_set_set = item_set_tran_list.item_set_set; // 一元集合的集合
ItemSetList transaction_list = item_set_tran_list.transaction_list;
ItemSetCount total_items_count;
ItemSetSet one_cset = itemset_with_min_support(
transaction_list, item_set_set, minS, total_items_count);
vector<ItemSetSet> total_cset;
ItemSetSet current_set = one_cset;
int k = 2;
while (not current_set.empty()) {
total_cset.push_back(current_set);
current_set = join_set(current_set, k);
current_set = itemset_with_min_support(transaction_list, current_set,
minS, total_items_count);
k++;
}
auto get_support = [&](ItemSet item_set) {
return (double)total_items_count[item_set] /
(double)transaction_list.size();
};
AprioriResult result;
for (auto &k_set : total_cset) {
for (auto &item_set : k_set) {
result.itemsWithSupport[item_set] = get_support(item_set);
}
}
for (auto k_set = total_cset.begin() + 1; k_set != total_cset.end();
k_set++) {
for (auto &item_set : *k_set) {
ItemSetSet subsets = get_subsets(item_set);
for (auto subset : subsets) {
ItemSet diff;
set_difference(item_set.begin(), item_set.end(), subset.begin(),
subset.end(), inserter(diff, diff.begin()));
if (diff.size() == 0) {
continue;
}
double confidence =
(double)get_support(item_set) / (double)get_support(subset);
if (confidence >= minC) {
result.rule[subset] = diff;
}
}
}
}
return result;
}
void print_result(const AprioriResult &result) {
cout << "Item set:" << endl;
vector<pair<ItemSet, double>> items(result.itemsWithSupport.begin(),
result.itemsWithSupport.end());
sort(items.begin(), items.end(),
[](const pair<ItemSet, double> &a, const pair<ItemSet, double> &b) {
return a.second > b.second;
});
for (auto item : items) {
for (auto i : item.first) {
cout << i << " ";
}
cout << ": " << item.second << endl;
}
cout << endl;
cout << "Rule:" << endl;
for (auto rule : result.rule) {
for (auto i : rule.first) {
cout << i << " ";
}
cout << "=> ";
for (auto i : rule.second) {
cout << i << " ";
}
cout << endl;
}
cout << endl;
}
int main() {
string file = "INTEGRATED-DATASET.csv";
double minS = 0.3;
cout << "Enter minimum support: ";
cin >> minS;
double minC = 0.4;
cout << "Enter minimum confidence: ";
cin >> minC;
AprioriResult result = run_apriori(file, minS, minC);
print_result(result);
}