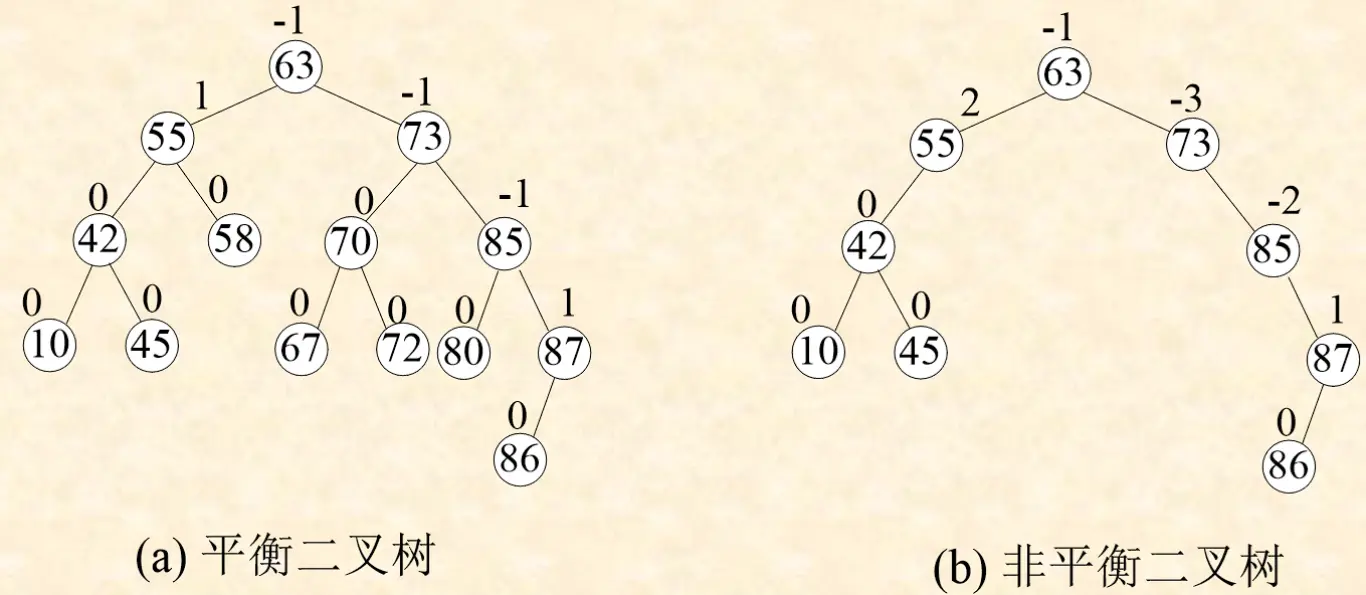
从上面简单的定义我们可以得出几个重要的信息:
- 平衡二叉树又称AVL 树
- 平衡二叉树必须是二叉排序树
- 每个节点的左子树和右子树的高度差至多为 1。
树的高度和深度
树的高度和深度本质区别:深度是从根节点数到它的叶节点,高度是从叶节点数到它的根节点。
指向原始笔记的链接
平衡因子= 左子树高度 - 右子树高度
旋转操作
左旋:
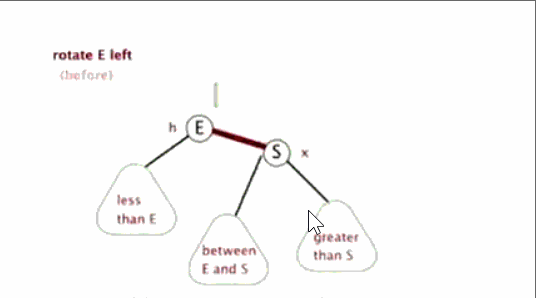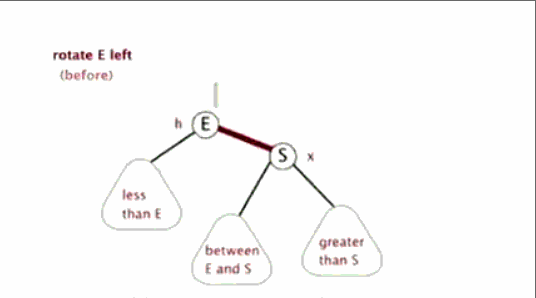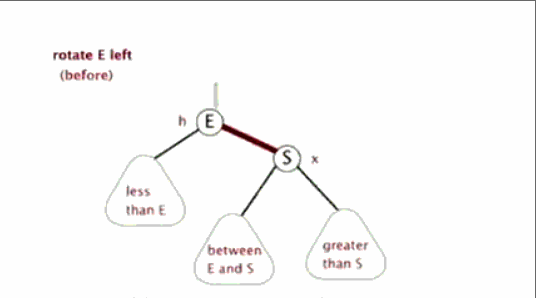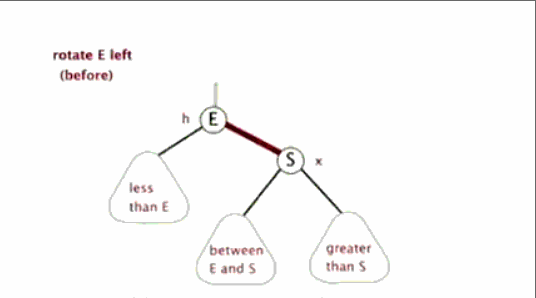
定义旋转中心是 E(将 E 左旋指的就是这个)。S 代替 E 作为根节点,S 左子树作为 E 的右子树,E 作为 S 左子树
作用是增大 E 和 S 的平衡因子,同时保持排序性质不变(E+2 或 +1(下面都平衡的情况),S+1)
右旋同理
插入
下面的 L 和 R 指的是多出来的位置,也就是插入的位置
插入的时候可能会有多个祖先节点出现失衡,只需要调整最近的一个就行
LL 型:
在插入位置往上找,第一个平衡因子为 2 的祖先 A,并且祖先的左孩子 B 的平衡因子为 1(可以判断这个时候在第一个失衡结点的左左处最长)
然后以 A 为中心右旋,旋转过后 AB 两个平衡因子都为 0

LR 型:

先左旋左孩子,再右旋自己(失衡位置)
删除
删除的话需要依次向上检查节点是否失衡,可能不止一次调整。删除的操作参考 二叉搜索树

