最长公共子序列

状态是两个字符串比较到的位置 $(i,j)$，在此位置的价值 d 定义为在此之前（包括这个位置）的公共子序列长度。

要使得末尾的 d 最大，找到子结构为状态 $(i,j)$ 来自于 $(i,j-1),(i-1,j-1),(i-1,j)$，根据这两个字符串在这个位置是否相等确定 d 最大能够取多少：如果不等，可能是 A 删掉这个的 d 或者 B 删掉这个字符的 d，如果相等，就是 $(i-1,j-1)$ 的 d 加一

def longestCommonSubsequence(str1, str2) -> int:
    def dp(i, j):
        # 空串的 base case
        if i == -1 or j == -1:
            return 0
        if str1[i] == str2[j]:
            # 这边找到一个 lcs 的元素，继续往前找
            return dp(i - 1, j - 1) + 1
        else:
            # 谁能让 lcs 最长，就听谁的
            return max(dp(i-1, j), dp(i, j-1))
        
    # i 和 j 初始化为最后一个索引
    return dp(len(str1)-1, len(str2)-1)

def longestCommonSubsequence(str1, str2) -> int:
    m, n = len(str1), len(str2)
    # 构建 DP table 和 base case
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    # 进行状态转移
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if str1[i - 1] == str2[j - 1]:
                # 找到一个 lcs 中的字符
                dp[i][j] = 1 + dp[i-1][j-1]
            else:
                dp[i][j] = max(dp[i-1][j], dp[i][j-1])
        
    return dp[-1][-1]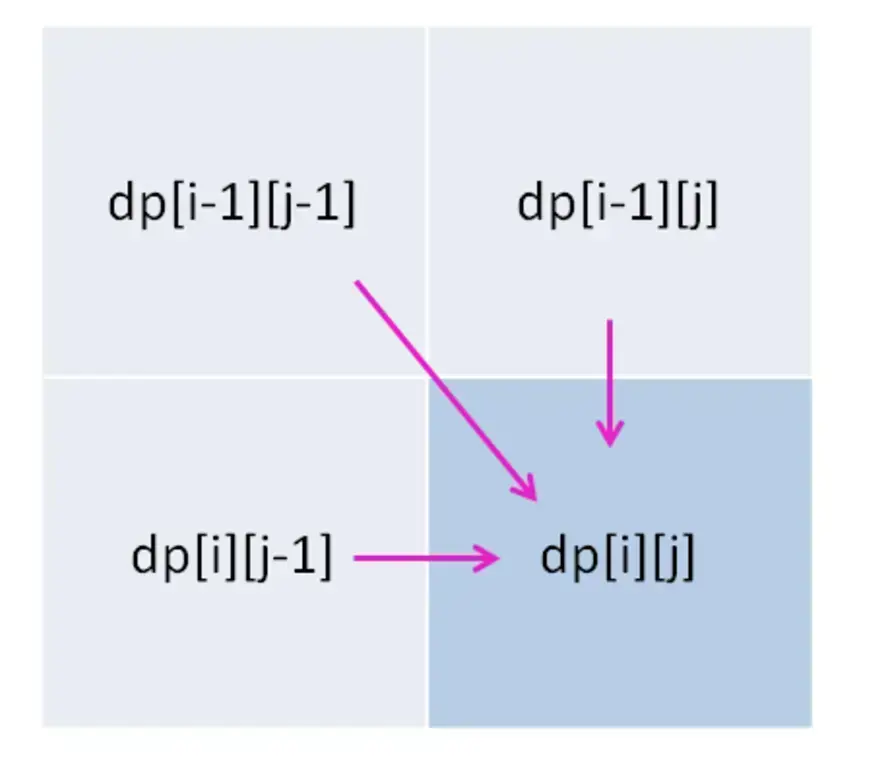

左上角转移右下角条件是两个字符串尾巴相等，否则就是上和左两个取大。因为左上永远小于其他，所以不考虑尾巴不相等的时候从左上转移的情况