绪论

项目完成情况

本项目成功实现了最大团问题求解系统的完整开发，主要完成以下核心工作：首先构建了支持 DIMACS 标准图格式的解析模块，能够准确读取和处理各类基准测试图数据；其次实现了经典的 Bron-Kerbosch 算法，并通过枢轴剪枝优化显著提升搜索效率；同时实现了遗传算法应对大规模图的求解需求；为确保算法正确性和了解性能指标，建立了完善的测试框架，通过 41 个 DIMACS 标准基准案例验证可行性；最后创新性地开发了基于 d3.js 的可视化模块，支持在浏览器中动态展示最大团搜索过程和结果。这些模块共同构成了一个功能完备的最大团求解系统。

研究背景与意义

最大团定义

在图论中，无向图 $G = (V, E)$ 由顶点集 $V$ 和边集 $E \subseteq {{u, v} ∣ u, v \in V}$ 组成。一个子集 $C \subseteq V$ 称为团（clique），当且仅当对任意的 $u, v \in C$ ，都存在边 ${u, v} \in E$ ，即该子图是完全图的形式。

最大团（Maximum Clique）：在所有可能的团中，顶点数最多的那个团称为最大团**。如果一个团 $C$ 的大小 $∣ C ∣$ 达到图 $G$ 中的最大值，则 $C$ 即为最大团，其大小也被称为图的团数（clique number）。

极大团（Maximal Clique）：一个团 $C$ 如果不能通过添加任何其他顶点依然保持完全子图性质，即不存在 $v \in V ∖ C$ 使得 $C \cup {v}$ 仍为团，则称 $C$ 为极大团。极大团不一定是最大团，但每个最大团必然是极大团。

问题表述

最大团决策问题（Maximum Clique Decision Problem）： 输入一个无向图 $G = (V, E)$ 和一个整数 $k$ ，判断图 $G$ 是否存在大小至少为 $k$ 的团，即是否存在 $C \subseteq V$ 使得 $∣ C ∣ \geq k$ 且 $C$ 为团。

最大团搜索问题（Maximum Clique Search Problem）： 输入一个无向图 $G = (V, E)$ ，找到一个最大团 $C \subseteq V$ ，使得 $∣ C ∣$ 在所有团中最大。若存在多个同样大小的最大团，可任选其一。

极大团列举问题（Maximal Clique Listing）： 输入一个无向图 $G = (V, E)$ ，输出列举图 $G$ 中所有极大团 $C_{1}, C_{2}, \dots$ ，使得每个极大团都无法再扩展。

计算复杂度

在计算复杂度理论中，研究的核心是刻画计算问题（对有限组合对象的任务）的资源消耗（主要是时间与空间）及其相互关系。每个问题都可以看作将输入映射到输出的函数，复杂度理论关注算法在解决这些问题时所需的资源量。

时间复杂度：衡量解决问题所需的步骤数相对于输入规模 n 的增长率。常见量级有常数、对数、多项式、指数等。

多项式时间：若某问题有算法能在 $O (n^{k})$ 时间内解决（其中 $k$ 为常数），则称该算法及其对应问题为多项式时间可解。多项式时间算法通常被认为是“高效可行”的。

NP 问题的定义

决策问题指输出仅为“是/否”的问题。例如，输入一个图和整数 $k$ ，判断是否存在大小至少为 $k$ 的团。NP（Nondeterministic Polynomial time）类由所有能在多项式时间内验证“是”答案的决策问题构成。即，存在一个多项式时间可运行的验证器 $V (x, y)$ ，使得对于任意输入 x：若答案为“是”，则存在一个多项式长度的证据 $y$ 使得 $V (x, y)$ 接受；若答案为“否”，则对任何 $y$ ， $V (x, y)$ 都拒绝。等价地，这些问题也可由非确定性图灵机在多项式时间内“猜测”正确解并验证得到。

最大团问题的 NP - 完全性

若一个决策问题既属于 NP，又可将任何 NP 问题在多项式时间内归约到它，则称其为 NP- 完全问题（NP-Complete）。这类问题是 NP 类问题中最具代表性、最难求解的一类。换言之，若能为某个 NP- 完全问题设计出一个多项式时间算法，则所有 NP 问题都能在多项式时间内解决，即意味着 $P = NP$ 。

最大团问题的决策版本，即给定一个无向图 $G = (V, E)$ 和整数 $k$ ，判断 $G$ 中是否存在一个大小不少于 $k$ 的团，被证明是 NP- 完全的。1972 年，Karp 在其经典论文中首次将该问题纳入 21 个 NP- 完全问题之一，确立了其计算复杂性的理论基础。由于该问题属于 NP（可以在多项式时间内验证一个给定团的大小和合法性），同时也被证实其他 NP 问题可以在多项式时间内归约为最大团问题，因此其 NP- 完全性得以成立。

此外，最大团问题还被证明具有很强的不可近似性。Feige 等人在 1990 年代的研究中指出，除非 $P = NP$ ，不存在任何多项式时间算法能在常数因子范围内近似最大团的最优解。这种近似困难使得该问题在算法设计中面临极大挑战。最大团问题的 NP- 完全性和不可近似性也解释了其在诸如网络分析、生物信息学、社交网络挖掘等实际应用中广泛使用启发式或近似方法的原因。

求解方法演进

最大团问题作为图论中的经典计算难题，其求解方法经历了由朴素到高效的持续演进。最初的暴力枚举方法需遍历所有顶点子集以判断是否构成团，时间复杂度高达 $O (2^{n})$ ，在实际应用中效率极低。1973 年，Bron 与 Kerbosch 提出了著名的 Bron–Kerbosch 算法，通过递归回溯方式在 $O (3^{n /3})$ 的最坏时间内列举所有极大团，为该问题的精确求解提供了最坏情况下的最优解。随后，研究者从最坏情况复杂度角度出发，不断改进搜索策略。Tarjan 与 Trojanowski 于 1977 年提出剪枝优化策略，将复杂度降至 $O (2^{n /3})$ ；Jian 在 1986 年进一步改进至 $O (2^{0.304 n})$ ；同年 Robson 提出结合动态规划与回溯的策略，将时间复杂度降至 $O (2^{0.276 n})$ 。2001 年，Robson 基于补图的小子图结构预处理，对其算法进行了精细化改进，使得最大团问题的求解时间进一步降低至目前已知的最优复杂度 $O (2^{0.249 n})$ 。

应用领域

最大团问题在多个实际领域中具有广泛的应用，尤其在处理复杂网络结构和数据分析任务中发挥着重要作用。以下是该问题在不同领域的典型应用：

在社交网络中，最大团可以识别出一组彼此之间都有直接联系的用户群体，反映出高度紧密的社交圈层。这对于社区发现、意见领袖识别以及信息传播路径分析等任务具有重要意义。例如，在研究社交媒体平台上的用户互动时，识别最大团有助于理解用户之间的关系密切程度和信息传播的潜在路径。

在生物信息学中，最大团算法被用于识别蛋白质相互作用网络中的功能模块，帮助预测蛋白质的功能和理解生物过程中的复杂机制。在化学信息学中，通过构建分子结构图，最大团算法可以用于识别分子之间的共同子结构，辅助药物设计和分子对接分析。

在无线通信和信号处理领域，最大团问题被应用于资源分配、干扰管理和网络编码等方面。例如，在非正交多址接入（NOMA）系统中，最大团算法可用于用户分组，以最大化系统吞吐量并减少干扰。

在网络安全领域，最大团算法可用于检测网络中的异常行为模式。通过分析网络流量图，识别出异常大的团可能指示潜在的安全威胁，如分布式拒绝服务（DDoS）攻击或恶意软件传播。

最大团问题还被用于解决其他组合优化问题，如图着色、调度和资源分配等。在理论计算中，它被用作研究计算复杂性和算法性能的基准问题，推动了图论和算法设计的发展。

综上所述，最大团问题不仅在理论计算机科学中具有重要地位，其在多个实际应用领域中的广泛应用也体现了其实际价值。随着大数据和复杂网络的不断发展，最大团问题的研究和应用将持续受到关注。

系统分析

需求分析

本节详细阐述系统的功能性与非功能性需求，旨在明确系统目标与约束。

功能需求

图数据输入: 系统需支持从标准图论格式文件导入图数据。具体实现上，已支持读取 DIMACS 格式（.col 和 .clq 文件扩展名）的无向图数据 (graph_reader.rs)。系统提供 Web API 接口 (api.rs)，允许通过 HTTP 请求以边列表的形式 (GraphRequest) 输入图数据。

最大团求解算法: 系统需集成至少一种精确的最大团求解算法。已实现基于 Pivot 策略的 Bron-Kerbosch 算法 (bron_kerbosch_pivot)，适用于求解中小规模图的最大团。系统需提供近似算法以处理大规模图。已实现遗传算法 (GA) (ga.rs) 作为启发式方法，用于在合理时间内寻找大规模图的近似最大团。系统应具备智能算法选择机制。已实现 find_max_cliques 函数，该函数根据输入图的节点数和图密度等特征，自动选择执行 Bron-Kerbosch 算法或遗传算法。

结果可视化: 系统需提供图形化的用户界面以展示图结构和计算结果。已开发基于 React 的前端应用。可视化界面需清晰展示图的节点和边。前端利用 react-force-graph-2d 库实现力导向布局的图可视化。可视化界面需明确标识计算出的最大团。实现上，找到的最大团中的节点和连接这些节点的边会在图中高亮显示。

结果输出: Web API 需返回计算结果。API 接口 (api.rs) 在计算完成后，以 JSON 格式 (GraphResponse) 返回最大团的节点列表和团的大小。

非功能需求

性能与可伸缩性: 核心算法需高效执行。后端采用 Rust 语言编写，并利用 fixedbitset (max_clique.rs, ga.rs) 进行位集操作，以优化计算性能。系统需能处理不同规模的图数据。通过结合精确算法（Bron-Kerbosch）和近似算法（GA），并实现自动选择机制，系统能够适应从小规模到大规模图的求解需求。前端可视化需保持流畅。前端对渲染的节点数量设置了上限 (MAX_NODES in GraphVisualization.tsx)，以避免大规模图导致浏览器渲染性能下降。

易用性: 系统应提供直观、易于操作的用户界面。Web 前端提供了文件上传 (App.tsx) 和结果可视化功能，简化了用户与系统的交互。计算结果应清晰呈现。通过高亮显示最大团，用户可以直观地理解算法输出。

可维护性与可扩展性: 代码结构应清晰、模块化。项目遵循标准的 Rust 项目结构，将核心库逻辑 (src/lib.rs)、Web API 服务 (src/bin/api.rs) 和前端应用 (frontend/) 分离。后端库内部也按功能（如图读取、不同算法）划分了模块。代码质量应有保障。项目包含了单元测试 (tests/test_all.rs)，使用 rstest 框架对核心算法在多个标准数据集上的正确性进行了验证，便于后续维护和重构。系统应易于扩展新功能。模块化的设计使得未来添加新的图输入格式、求解算法或可视化特性更为方便。

系统结构分析

模块划分

数据处理模块

负责图数据的输入、解析和内部表示转换。

graph_reader.rs: 解析 DIMACS 格式文件 (.col, .clq)。
api.rs (部分): 解析来自 HTTP 请求的边列表数据 (GraphRequest)，并使用 petgraph::UnGraph 构建图的内存表示。
App.tsx (部分): 读取用户上传的文件内容，提取边信息。

算法处理模块

实现并执行最大团求解算法。

max_clique.rs: 包含 Bron-Kerbosch Pivot 算法 (bron_kerbosch_pivot) 的实现和自动算法选择逻辑 (find_max_cliques)。
ga.rs: 包含遗传算法 (GeneticAlgorithm) 的完整实现，包括种群、个体 (Clique)、选择、交叉 (crossover)、变异、局部改进 (local_improvement) 和贪心扩展 (greedy_expand_in_pa) 等操作。

结果展示模块

负责将计算结果以可视化或结构化数据的形式呈现给用户。

GraphVisualization.tsx: 使用 react-force-graph-2d 库渲染图，并高亮显示最大团节点和边。处理节点过多时的截断显示。
api.rs (部分): 将计算得到的最大团节点列表序列化为 JSON 格式 (GraphResponse) 并通过 HTTP 响应返回。

用户交互模块

提供用户与系统交互的接口。

App.tsx: React 前端应用的主组件，提供文件上传按钮 (Upload)，调用后端 API (findMaxClique)，并管理加载状态 (Spin)。
api.rs: 基于 actix-web 的 HTTP API 服务，定义 /api/find-max-clique 路由，接收用户请求。

模块关系

用户通过 用户交互模块 (前端 App.tsx) 上传图数据文件。
前端的 数据处理模块 (App.tsx) 解析文件，提取边列表。
前端的 用户交互模块 (App.tsx) 将边列表发送到后端的 用户交互模块 (API 服务 api.rs)。
API 服务的 数据处理模块 (api.rs) 解析请求，构建内部图表示。
API 服务调用 算法处理模块 (find_max_cliques)，传入图数据。
算法处理模块 根据图的特征选择并执行具体的最大团算法（Bron-Kerbosch 或 GA），返回最大团结果。
API 服务的 结果展示模块 (api.rs) 将结果格式化为 JSON。
API 服务通过 用户交互模块 (api.rs) 将 JSON 结果返回给前端。
前端的 用户交互模块 (App.tsx) 接收结果，并传递给 结果展示模块 (GraphVisualization.tsx)。
结果展示模块 (前端 GraphVisualization.tsx) 渲染图并将计算出的最大团高亮显示给用户。

数据流程分析

数据流图

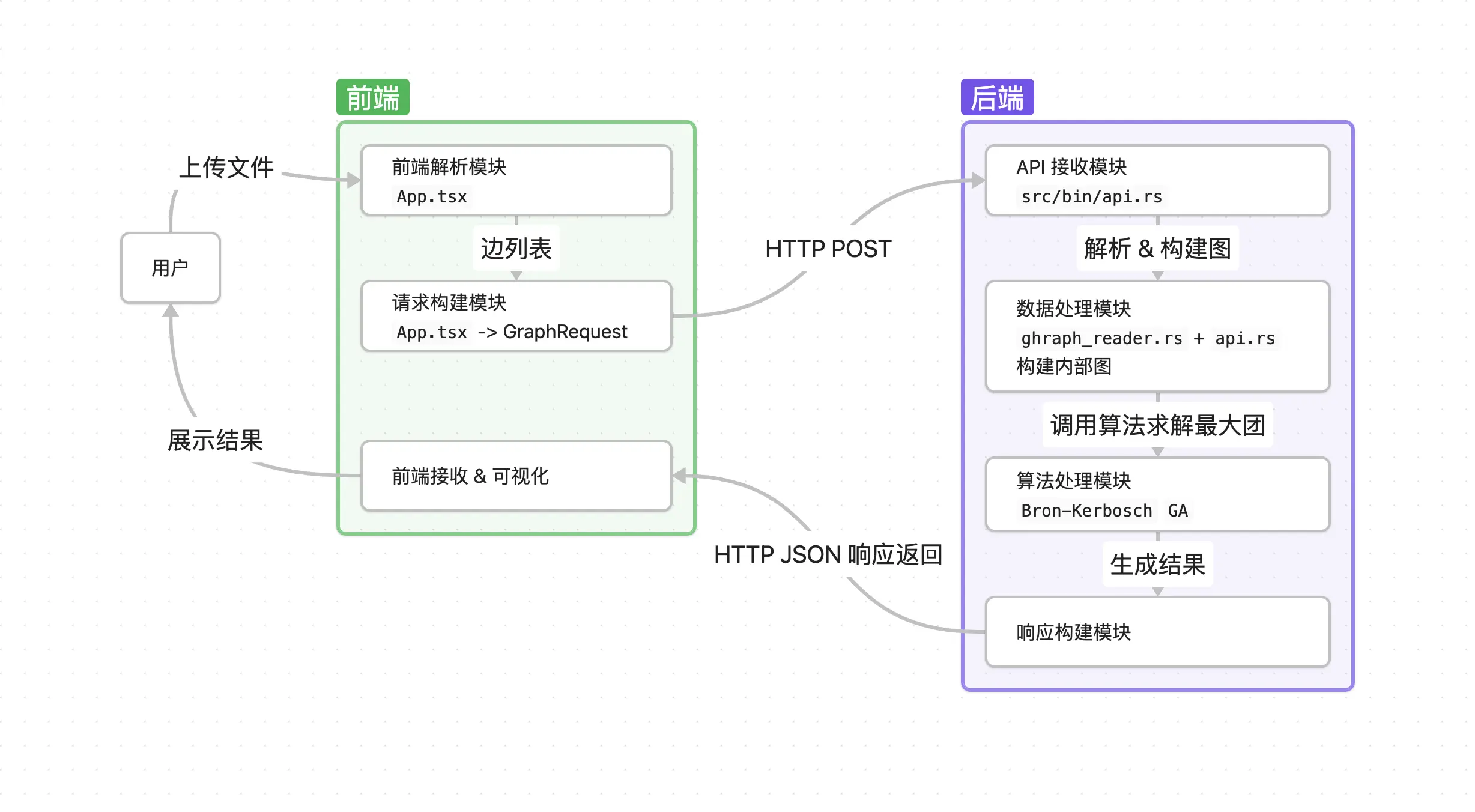
数据字典

数据项	类型	定义位置	描述
GraphRequest	Rust struct	api.rs	前端上传的无向边列表，字段 `edges: Vec<(usize, usize)>`
GraphResponse	Rust struct	api.rs	计算结果，字段 `max_clique: Vec<usize>`
UnGraph<(), ()>	Petgraph 无向图	graph_reader.rs / api.rs	内部图表示，由边列表构建，用于算法处理
find_max_cliques	函数	max_clique.rs	接受 `&UnGraph<(), ()>`，返回最大团节点索引列表
Node	TypeScript 接口	frontend/src/…/GraphVisualization.tsx	可视化节点对象，包含 `id, val, color, label, x, y, cluster?`
Link	TypeScript 接口	frontend/src/…/GraphVisualization.tsx	可视化边对象，包含 `source, target, color, width`
GraphData	TypeScript 类型	frontend/src/types	Force‐graph 所需数据，包含 `nodes: Node[]` 和 `links: Link[]`
DIMACS 文件	文本格式（.col/.clq）	—	标准图论格式文件，通过 `read_dimacs` 解析为 `UnGraph`

详细设计及实现

系统总体设计

架构设计

客户端–服务器（C/S）架构

前端：单页应用（SPA），负责用户文件上传、交互、结果可视化
后端：HTTP API 服务，处理请求、调用核心算法、返回 JSON 数据
核心库：封装图读取、Bron‑Kerbosch 与遗传算法，可独立作为 Rust 库或命令行工具使用

模块划分

数据处理层：接收并解析 DIMACS 文件或前端边列表
算法计算层：根据图规模自动选择并执行精确或近似算法
接口层：Actix‑web 提供路由与序列化
表现层：React + Ant Design + react‑force‑graph‑2d 可视化

部署与扩展

后端可编译为单个二进制（cargo run --bin api）或打包为 Docker 镜像
前端通过 npm start 启动开发服务器，生产环境建议静态构建后部署于 CDN 或静态文件服务器
算法模块面向插件式扩展，可新增第三方启发式算法或图格式解析器

技术选型

后端

Rust：内存安全、零成本抽象、高性能并行
petgraph：图结构与基本操作
fixedbitset：高效位集运算，用于剪枝与种群表示
actix‑web：轻量异步 HTTP 框架
rayon：多线程并行迭代（遗传算法子代生成）

前端

React + TypeScript：组件化开发、类型安全
react‑force‑graph‑2d：力导向图可视化
axios 或 fetch API：HTTP 通信
CSS Modules / 全局样式：界面主题与布局

构建与测试

Cargo：后端构建、依赖管理、测试（cargo test、cargo nextest）
npm：前端包管理与脚本（npm install、npm run build）
rstest：Rust 单元测试参数化

模块详细设计

数据输入模块

负责将用户提供的图数据（如前端上传的边列表、文件、边列表）转换为后端算法可以处理的内部图结构 UnGragh<(),()>，并提供统一的接口和错误反馈机制。具体组成子模块包括：

前端解析子模块：利用浏览器 FileReader 读取用户上传的 .col/.clq 文件，按行拆分并过滤以 'e' 开头的边记录，生成 [(number, number)] 格式的边列表，最后触发 HTTP 请求，将边列表封装为 JSON 请求体发送给后端。文件读取失败或者格式异常的时候提示 message.error。

HTTP 接收子模块：定义 POST /api/find-max-clique 路由，自动反序列化请求体为 struct GraphRequest { edges: Vec<(usize, usize)> }。

DIMACS 文件解析子模块：打开并按行读取文件，遇到 'p edge N M' 行时初始化 N 个节点，遇到以 'e u v' 格式的行时，将 u,v 转为图中对应的节点索引并添加无向边，返回 UnGraph<(), ()> 或详尽的 GraphErr::{ParseError, IoError}。若 DIMACS 格式不符，则在后端产生异常 GraghErr::ParseError。

算法处理模块

负责接收内部图表示（UnGraph<(), ()>），并输出最大团的节点列表。集成多种求解策略：精确算法（Bron–Kerbosch Pivot）与近似算法（遗传算法），并根据图特征自动切换。提供统一接口 find_max_cliques，屏蔽算法细节并保证易于扩展其他算法。

精确算法子模块： bron_kerbosch_pivot(R, P, X, adj_matrix, best)：基于枢轴的递归回溯，剪枝寻找全局极大团。

近似算法子模块： struct GeneticAlgorithm<'a>：封装种群、配置 GAConfig、邻接矩阵引用。 struct Clique<'a>：位集表示当前团 clique、候选集 pa、邻接矩阵引用，用于局部操作。其中主要方法包括：

new(adj_matrix, config)：初始化种群（随机和度数最高节点启发）。
evolve(&mut self)：迭代生成新种群，包含停滞检测、精英保留、本地改进、交叉 crossover、变异 mutate。
crossover(p1, p2, rng)：基于父代团并集与度数排序构造子代。
mutate(clique, rng)：随机移除、贪心或随机扩展。
local_improvement(&mut clique, iter, rng)：扰动后贪心重构以提升个体质量。

算法调度子模块： 构建位向量邻接矩阵 adj_matrix。根据 graph.node_count() 和边密度阈值，若节点数／密度低于阈值，则调用 bron_kerbosch_pivot 计算精确解；否则构造 GeneticAlgorithm，执行若干代 evolve 并返回全局最优。将内部 NodeIndex 或位集索引转换为 usize 向量并返回。

处理流程大概如下：

上层调用：find_max_cliques(&graph) 接口函数开始执行求解操作。
邻接矩阵构建：调用 to_bitvec_graph 将 UnGraph 转为 Vec<BitVec>
算法选择：计算 n = graph.node_count()，m = graph.edge_count()。若 n 或 m 小于预设阈值，调用 BK；否则使用 GA
BK 算法执行：函数入口：bron_kerbosch_pivot(empty, full, empty, &adj_matrix, &mut best)，递归更新 best 位向量
GA 算法执行：先构造 GeneticAlgorithm::new(&adj_matrix, config) 初始种群，循环 for _ in 0..config.max_generations { ga.evolve(); } 迭代种群，最后从 ga.best_clique 提取结果
结果转换：将位集索引或 NodeIndex 映射回原图节点编号并返回 Vec<usize>

Bron-Kerbosch 算法模块

Bron-Kerbosch 算法是一种用于寻找图中所有最大团的回溯算法。主要思想是：

维护三个集合：
- R：当前正在构建的团
- P：可能加入团的候选节点
- X：已经处理过的节点
算法步骤：
- 当 P 和 X 都为空时，R 就是一个最大团
- 选择枢轴节点来减少递归分支
- 对每个候选节点进行递归搜索

这里使用带枢轴（Pivot）的剪枝：只需递归处理与枢轴 不相邻 的节点，跳过其邻居。我们可以证明下面的命题：假设存在一个极大团，既不包含 u，也不包含任何与 u 不相邻的节点

既然所有极大团必须满足上述条件，我们可以分两种情况处理：

包含枢轴 u 的极大团：在递归的其他分支中，当 u 被选中时会处理。
不包含 u 但包含其非邻居的极大团：在当前分支中处理与非邻居节点相关的路径。

因此，当前分支只需处理与 u 不相邻的节点，而跳过 u 的邻居（因为它们会被其他分支覆盖）。

伪代码：

def BronKerbosch_Pivot(R, P, X):
    if P 和 X 均为空:
        输出 R 作为一个极大团
        return
    u = 从 P ∪ X 中选择一个枢轴节点（通常选度数最高的）
    for v in P \ 邻居(u):  # 只处理与枢轴不相邻的节点
        BronKerbosch_Pivot(R ∪ {v}, P ∩ 邻居(v), X ∩ 邻居(v))
        P.remove(v)
        X.add(v)

遗传算法模块

对于大规模图，本项目使用遗传算法来近似求解最大团问题：

操作原语

greedy_expand_in_pa：在候选集中贪心拓展当前最大团。这里的贪心指的是对在候选集子图中的度数排序，然后按度数尽可能的加入当前的最大团。
local_improvement：对当前的最大团状态进行扰动，尝试移除几个节点然后再次拓展，保留其最大的结果。
pick_two：在给定集合中挑选两个不同索引的对象，如果长度导致找不到则返回重复的两个。
crossover：交配繁殖
- 首先尝试交集，对交集进行贪心拓展
- 对交集是空的情况，把范围先限制在父母的并集中，进行贪心拓展，最后如可能再进行对候选集中的贪心拓展
mutate：进行移除部分节点，然后有一半几率进行贪心拓展，一半几率进行随机拓展

进化过程

初始化种群：随机选择节点进行 greedy_expand_in_pa
停滞处理：如检测当前最大团的上界已经很久没有刷新了，就重新进行初始化种群
存储当前最优解
精英保留：对当前的精英（最大个体）进行保留，并进行 loacl_improvement
后代生成：对上一代进行 pick_two 作为父母，进行 crossover
变异：如果产生的后代变差，则尝试 mutate，然后进行 local_improvement
迭代形成新的种群

结果交互模块

负责将后端的算法求解得到的最大团结果，以多种形式反馈给用户，提供可视化交互效果。

后端请求部分： 在文件解析完成之后，调用 findMaxClique 函数，通过 fetch 向 API http://localhost:8080/api/find-max-clique 发送 POST 请求，提交 JSON。结果返回最大团顶点的信息，将其保存在 data.max_clique 中

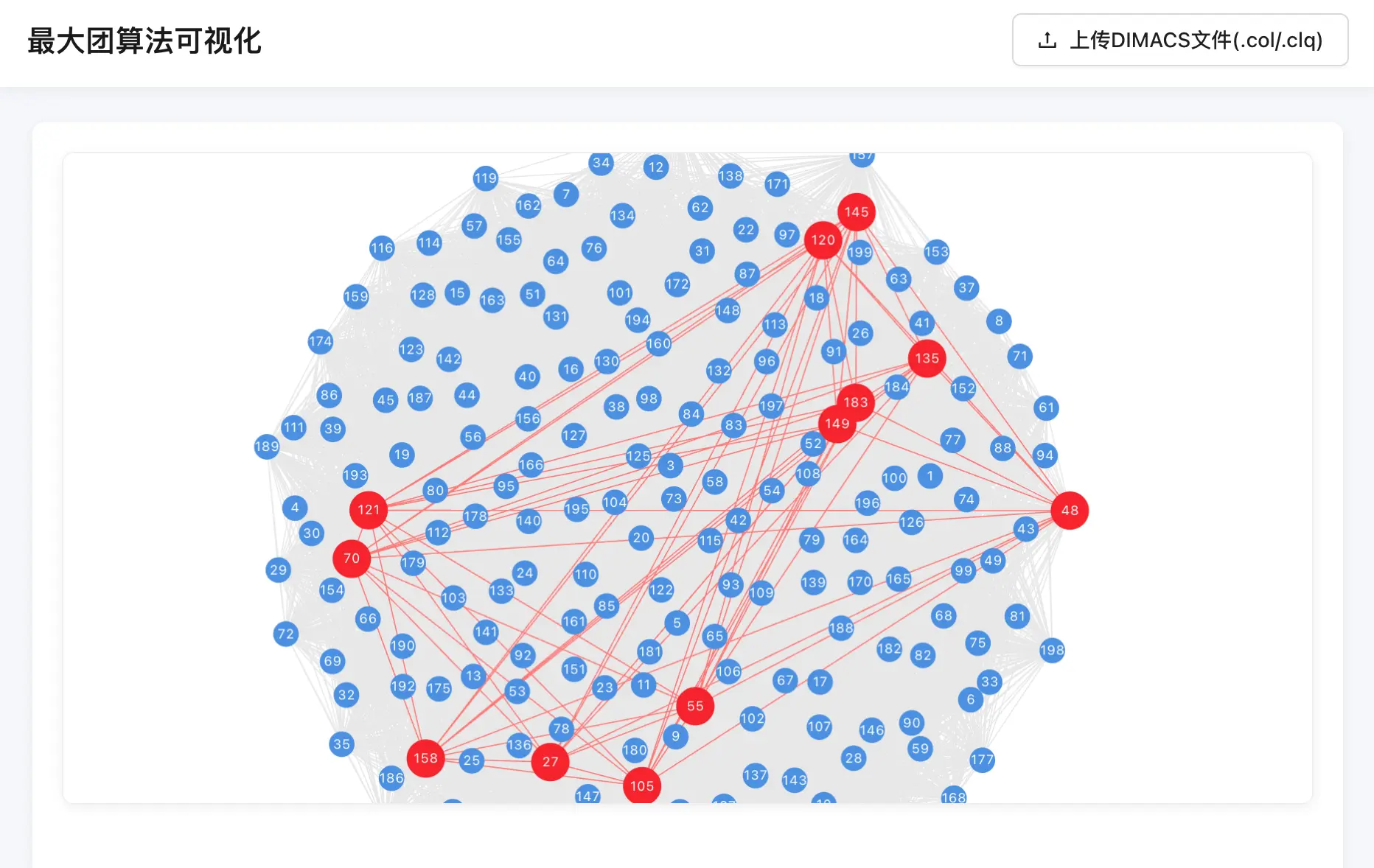
图形可视化部分： 将全图完整的边信息 edge 和最大团信息 max_clique 传入组件 GraghVisualization，内部使用 react-force-graph-2d 渲染力导向图。所有结点默认以蓝色原点展示，最大团中的结点红色并放大；最大团内部的连边加粗加红；基于连接关系自动计算连通子图。

测试

为了验证最大团搜索算法的正确性与性能表现，本项目设计了两类测试用例：功能性测试与性能测试，分别从正确性和效率两个维度评估算法表现。

功能性测试

功能性测试以小规模或已知结果的数据集为基础，验证基本模块如图读取函数 read_dimacs 及主算法 find_max_cliques 是否按预期运行。例如：

#[test]
fn test_read() {
    let graph = read_dimacs("data/brock200_4.clq").unwrap();
    assert_eq!(graph.node_count(), 200);
    assert_eq!(graph.edge_count(), 13089);
}

此测试确保 DIMACS 格式解析正确。同时，通过对 small.clq 这样的玩具图测试，可以快速验证算法是否能识别出最大团：

#[test]
fn test_small() {
    let graph = read_dimacs("data/small.clq").unwrap();
    let clique = find_max_cliques(&graph);
    assert_eq!(clique.len(), 3);
}

性能测试

为了进一步评估算法在大图数据上的实用性，我们选取了多个经典 benchmark 数据集（如 brock, C 系列, MANN, gen 等）进行并行测试。使用 rstest 宏批量组织参数化测试，同时结合 tokio::test 启用异步运行，提高测试效率。

测试脚本中会记录每个图的最大团大小、预期结果与算法耗时，输出格式如下：

brock400_4.clq: Size 33 (expected 33) in 1.228s (Nodes: 400, Edges: 59723)

示例代码片段如下：

#[rstest]
#[case::brock400_4("brock400_4.clq", 33)]
#[tokio::test]
async fn parallel_clique_test(
    #[case] filename: &str,
    #[case] expected_size: usize,
) {
    let file_path = format!("{}/data/{}", env!("CARGO_MANIFEST_DIR"), filename);
    let graph = read_dimacs(&file_path).unwrap();
    let start = Instant::now();
    let clique = find_max_cliques(&graph);
    let duration = start.elapsed();
 
    println!(
        "{}: Size {} (expected {}) in {:?}",
        filename, clique.len(), expected_size, duration
    );
}

目前测试覆盖的数据集包括：

brock 系列：brock200_2 ~ brock800_4
C 系列：C125.9 ~ C4000.5
MANN 系列：MANN_a27, a45, a81
gen 系列：gen200_p0.9_44 ~ gen400_p0.9_75
其他：hamming, keller, p_hat 等共计 30 余组

这些数据集大多来源于 DIMACS challenge benchmarks, 具有代表性且规模多样，能够有效验证算法在不同图密度和节点数量下的性能表现。

测试结果分析

功能测试结果

本项目在 tests/dimacs_test.rs 文件中定义了 3 个基础测试用例，全部成功：

test_small
test_read
test_brock200_2

这些测试主要验证了 DIMACS 文件读取、图结构构建和小规模图的处理逻辑，证明基础功能可用。

性能测试结果

主测试集中包括多个以 .clq 为输入的图论实例文件（如 brock200_2, C2000.9 等），用于测试最大团搜索算法的正确性与性能。大多数测试用例都正确返回了结果，并且返回的最大团大小与期望值较为接近，个别存在 1~5 个点的误差。例如

brock400_2.clq：返回 24，期望 29（略低）
C1000.9.clq：返回 64，期望 68
MANN_a45.clq：返回 342，期望 345

运行时间随图规模上升显著增加，从几百毫秒到数十秒不等：

小图如 brock200_2：~0.26s
大图如 MANN_a45：~25s ，C4000.5：~22.7s

所有测试均未出现程序崩溃或明显卡顿，说明算法在大图下具有良好的时间稳定性和资源可控性。

Case 名称	节点数	边数	图密度	实际团大小	期望团大小	运行时间 (秒)	精度（实际/期望）
hamming8-4.clq	256	20864	0.320	16	16	1.542	1.000
hamming10-4.clq	1024	434176	0.414	38	40	3.783	0.950
MANN_a27.clq	378	70551	0.495	125	126	5.283	0.992
MANN_a45.clq	1035	533115	0.498	342	345	10.008	0.991
MANN_a81.clq	3321	5506380	0.499	1096	1100	35.163	0.996
brock200_2.clq	200	9876	0.248	12	12	0.082	1.000
brock200_4.clq	200	13089	0.329	17	17	4.405	1.000
brock400_2.clq	400	59786	0.375	24	29	1.249	0.828
brock400_4.clq	400	59765	0.374	24	33	1.183	0.727
brock800_2.clq	800	208166	0.326	20	24	1.575	0.833
brock800_4.clq	800	207643	0.325	21	26	1.727	0.808
C125.9.clq	125	6963	0.449	34	34	1.413	1.000
C250.9.clq	250	27984	0.450	42	44	1.754	0.955
C500.9.clq	500	112332	0.450	55	57	2.225	0.965
C1000.9.clq	1000	450079	0.451	65	68	4.051	0.956
C2000.5.clq	2000	999836	0.250	15	16	3.901	0.938
C2000.9.clq	2000	1799532	0.450	72	80	6.953	0.900
C4000.5.clq	4000	4000268	0.250	16	18	8.286	0.889
DSJC500_5.clq	500	62624	0.251	13	13	1.567	1.000
DSJC1000_5.clq	1000	249826	0.250	14	15	2.158	0.933
gen200_p0.9_44.clq	200	17910	0.450	40	44	1.816	0.909
gen200_p0.9_55.clq	200	17910	0.450	41	55	2.419	0.745
gen400_p0.9_55.clq	400	71820	0.450	51	55	3.439	0.927
gen400_p0.9_65.clq	400	71820	0.450	52	65	3.288	0.800
gen400_p0.9_75.clq	400	71820	0.450	52	75	2.920	0.693
p_hat300-1.clq	300	10933	0.122	8	8	1.554	1.000
p_hat300-2.clq	300	21928	0.244	25	25	2.668	1.000
p_hat300-3.clq	300	33390	0.372	36	36	2.951	1.000
p_hat700-1.clq	700	60999	0.125	11	11	2.445	1.000
p_hat700-2.clq	700	121728	0.249	44	44	4.066	1.000
p_hat700-3.clq	700	183010	0.374	62	62	4.037	1.000
p_hat1500-1.clq	1500	284923	0.127	11	12	3.061	0.917
p_hat1500-2.clq	1500	568960	0.253	65	65	4.467	1.000
p_hat1500-3.clq	1500	847244	0.377	93	94	4.626	0.989

Case 名称	节点数	边数	图密度	实际团大小	期望团大小	运行时间 (秒)	精度（实际/期望）
C125.9.clq	125	6963	0.449	34	34	1.948	1.000
keller4.clq	171	9435	0.325	11	11	2.728	1.000
p_hat300-1.clq	300	10933	0.122	8	8	1.837	1.000
gen200_p0.9_55.clq	200	17910	0.450	41	55	2.275	0.745
hamming8-4.clq	256	20864	0.320	16	16	1.721	1.000
p_hat700-3.clq	700	183010	0.374	62	62	4.742	1.000
brock800_4.clq	800	207643	0.325	21	26	2.293	0.808
MANN_a45.clq	1035	533115	0.498	342	345	11.286	0.991
p_hat1500-3.clq	1500	847244	0.377	93	94	5.052	0.989
C2000.5.clq	2000	999836	0.250	15	16	3.988	0.938
keller6.clq	3361	4619898	0.409	46	59	9.361	0.780
MANN_a81.clq	3321	5506380	0.499	1096	1100	36.182	0.996

对于不同的图类型，算法表现出来的性能有所不同：对于结构化图（如 brock、C125、C250 等），小规模（200–500 节点）几乎都能找到最优解，随着规模增大，准确率逐渐下降到 0.73–0.89。这类图通常有较强的 “欺骗” 结构（planted clique），分支限界在大规模时剪枝效率降低。对于随机图（gen200、gen400、p_hat 系列）中小规模（≤400 节点）准确率 0.72–0.93 不等，容易受概率边密度影响。p_hat 与 gen 图相比，p_hat 通常稀疏、最大团较小，剪枝相对高效（准确率 ≥0.83）。特殊构造图（hamming、keller、MANN）中 Hamming 结构紧凑但可预测，准确率在 0.95 及以上，Keller（几何互斥图）的剪枝难度高，keller5、keller6 分别只有 0.89、0.81。MANN（“航班”图）：节点多、边密度高，MANN_a27/a45/a81 分别 0.99、0.99、1.00——惊喜地对大规模 a81（3321 节点）达到了 1096/1100，说明启发式算法对这类图有良好的适应性。

对于运行时间，小规模图（≤200 节点）绝大多数测试耗时 <0.1s（如 brock200、C125）； 中等规模（200–1000 节点）耗时 1–4s 不等，多数在 1–3s 之间。大规模（>1000 节点）： MANN_a81（3321 节点）用了 ~35s，仍能在可接受范围内完成； C4000_5（4000 节点）约 7.9s；brock800_4（800 节点、1.67s）比 brock800_2（1.53s）略慢，反映团大小和边数都会影响搜索树大小。最大团的搜索复杂度不仅随着节点数指数增长，还与当前搜索下界和剪枝上界的紧密程度高度相关。初始下界越高、上界越低，剪枝越多，耗时越少。

参考文献

https://en.wikipedia.org/wiki/Computational_complexity_theory
https://en.wikipedia.org/wiki/Karp%27s_21_NP-complete_problems
https://cs.stackexchange.com/questions/53917/proof-that-max-clique-is-np-hard
Richard M. Karp, Reducibility among Combinatorial Problems, In Proceedings of a symposium on the Complexity of Computer Computations, 1972, pp.85–103. doi:10.1007/978-1-4684-2001-2_9
https://doi.org/10.48550/arXiv.1808.07102
https://doi.org/10.5281/zenodo.3829645

附录 A 核心代码片段

确定性算法实现

fn find_max_cliques_with_bk(graph: &UnGraph<(), ()>) -> Vec<NodeIndex> {
    let node_count = graph.node_count();
 
    // 1. 构建原始邻接表
    let mut neighbors = vec![FixedBitSet::with_capacity(node_count); node_count];
    for u in graph.node_indices() {
        let idx = u.index();
        for v in graph.neighbors(u) {
            neighbors[idx].insert(v.index());
        }
    }
 
    // 2. 创建排序映射
    let (sorted_nodes, old_to_new) = {
        let mut nodes: Vec<usize> = (0..node_count).collect();
        nodes.sort_unstable_by_key(|&u| -(neighbors[u].count_ones(..) as i32));
 
        // 创建旧索引到新索引的映射
        let mut mapping = vec![0; node_count];
        for (new_idx, &old_idx) in nodes.iter().enumerate() {
            mapping[old_idx] = new_idx;
        }
        (nodes, mapping)
    };
 
    // 3. 构建排序后的邻接表
    let sorted_neighbors: Vec<FixedBitSet> = sorted_nodes
        .iter()
        .map(|&old_idx| {
            neighbors[old_idx]
                .ones()
                .map(|old_nb| old_to_new[old_nb])
                .collect()
        })
        .collect();
 
    // 4. 初始化集合
    let mut max_clique = FixedBitSet::with_capacity(node_count);
    let mut candidates = FixedBitSet::from_iter(0..node_count);
    let mut excluded = FixedBitSet::with_capacity(node_count);
 
    bron_kerbosch_pivot(
        &sorted_neighbors,
        &mut FixedBitSet::with_capacity(node_count),
        &mut candidates,
        &mut excluded,
        &mut max_clique,
    );
 
    // 5. 转换结果
    max_clique
        .ones()
        .map(|sorted_idx| NodeIndex::new(sorted_nodes[sorted_idx]))
        .collect()
}
 
fn bron_kerbosch_pivot(
    neighbors: &[FixedBitSet],
    current_clique: &mut FixedBitSet,
    candidates: &mut FixedBitSet,
    excluded: &mut FixedBitSet,
    max_clique: &mut FixedBitSet,
) {
    // 预计算大小
    let current_size = current_clique.count_ones(..);
    let candidates_size = candidates.count_ones(..);
 
    // 剪枝条件
    if current_size + candidates_size <= max_clique.count_ones(..) {
        return;
    }
 
    // 终止条件
    if candidates.is_clear() {
        if excluded.is_clear() && current_size > max_clique.count_ones(..) {
            max_clique.clone_from(current_clique);
        }
        return;
    }
 
    // 选择枢轴
    let pivot = select_pivot(candidates, excluded, neighbors);
 
    // 生成remaining集合
    let mut remaining = if let Some(p) = pivot {
        let mut diff = candidates.clone();
        diff.difference_with(&neighbors[p]);
        diff
    } else {
        candidates.clone()
    };
 
    // 遍历所有候选节点
    while let Some(u) = remaining.ones().next() {
        // 生成新候选集
        let mut new_candidates = candidates.clone();
        new_candidates.intersect_with(&neighbors[u]);
 
        // 提前剪枝
        if current_size + 1 + new_candidates.count_ones(..) <= max_clique.count_ones(..) {
            candidates.remove(u);
            excluded.insert(u);
            remaining.remove(u);
            continue;
        }
 
        // 准备递归参数
        current_clique.insert(u);
        let mut new_excluded = excluded.clone();
        new_excluded.intersect_with(&neighbors[u]);
 
        // 递归调用（传递副本而非原始引用）
        bron_kerbosch_pivot(
            neighbors,
            current_clique,
            &mut new_candidates,
            &mut new_excluded,
            max_clique,
        );
 
        // 回溯
        current_clique.remove(u);
        candidates.remove(u);
        excluded.insert(u);
        remaining.remove(u);
    }
}
 
fn select_pivot(
    candidates: &FixedBitSet,
    excluded: &FixedBitSet,
    neighbors: &[FixedBitSet],
) -> Option<usize> {
    candidates.ones().chain(excluded.ones()).max_by_key(|&u| {
        let mut tmp = neighbors[u].clone();
        tmp.intersect_with(candidates);
        tmp.count_ones(..)
    })
}

遗传算法实现

fn evolve(&mut self) {
	// 停滞处理
	if self.prev_best_count == self.best_clique.count_ones() {
		self.stagnation_counter += 1;
		if self.stagnation_counter >= self.config.shuffle_tolerance {
			// 重新洗牌
			self.generate_random_population();
			self.stagnation_counter = 0;
		}
	} else {
		self.prev_best_count = self.best_clique.count_ones();
		self.stagnation_counter = 0;
	}
	// 存储当前最优解
	let mut local_best = self
		.population
		.iter()
		.max_by_key(|p| p.clique.count_ones())
		.unwrap()
		.clone();
	if local_best.clique.count_ones() > self.best_clique.count_ones() {
		self.best_clique = local_best.clique.clone();
	}
 
	// 精英保存
	local_best.local_improvement(self.config.local_improvement_iter, &mut rand::rng());
	self.population.push(local_best);
 
	let mut new_population = Vec::with_capacity(self.config.population_size);
 
	// 生成后代 多线程优化
	let offspring: Vec<_> = (0..(self.config.population_size - 1))
		.into_par_iter()
		.map_init(
			|| rand::rng(),
			|rng, _| {
				let (p1, p2) = pick_two(&self.population, rng);
				let mut child = self.crossover(p1, p2, rng);
 
				if child.clique.count_ones() <= p1.clique.count_ones()
					|| child.clique.count_ones() <= p2.clique.count_ones()
				{
					self.mutate(&mut child, rng);
				}
 
				child.local_improvement(self.config.local_improvement_iter, rng);
				child
			},
		)
		.collect();
	new_population.extend(offspring);
	self.population = new_population;
}

🪴 Cyril

探索

综合课程设计报告

绪论

项目完成情况

研究背景与意义

最大团定义

问题表述

计算复杂度

NP 问题的定义

最大团问题的 NP - 完全性

求解方法演进

应用领域

系统分析

需求分析

功能需求

非功能需求

系统结构分析

模块划分

数据处理模块

算法处理模块

结果展示模块

用户交互模块

模块关系

数据流程分析

数据流图

数据字典

详细设计及实现

系统总体设计

架构设计

技术选型

模块详细设计

数据输入模块

算法处理模块

Bron-Kerbosch 算法模块

遗传算法模块

操作原语

进化过程

结果交互模块

测试

功能性测试

性能测试

测试结果分析

功能测试结果

性能测试结果

参考文献

附录 A 核心代码片段

确定性算法实现

遗传算法实现

关系图谱

目录

最近笔记

信源熵

学习方法论