频繁模式与关联规则

实验内容简介

• 构建 FP-tree
• 构建条件模式树，根据条件模式树，输出所有的频繁模式
• 给出推理规则（关联规则）

算法说明

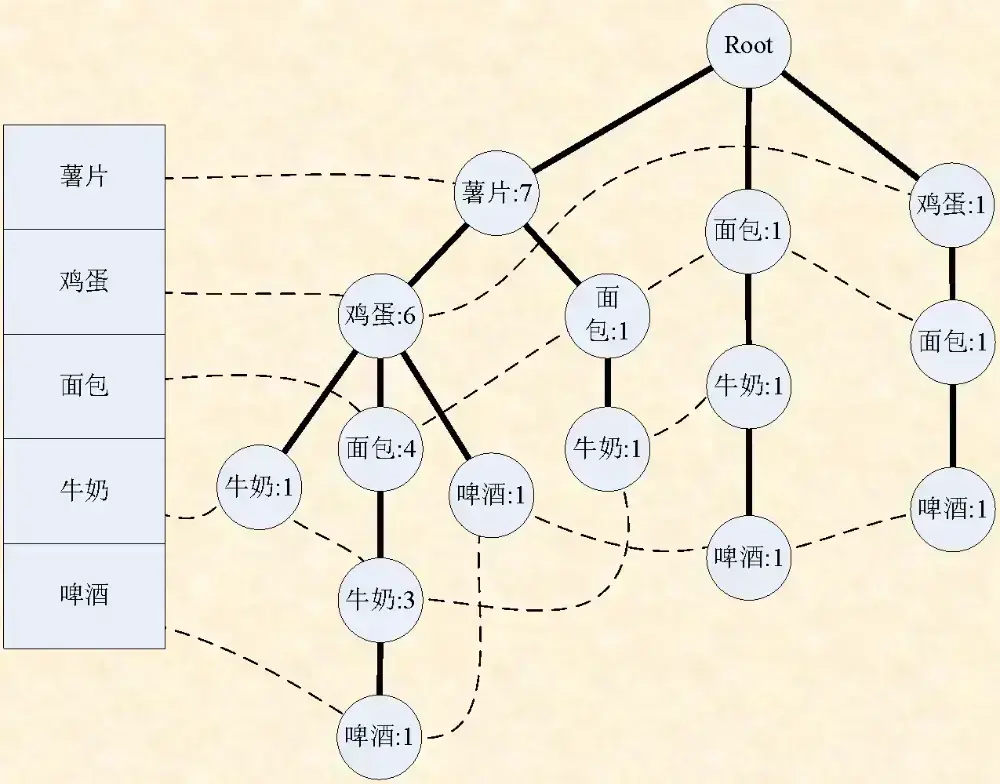
FP 树（Frequent Pattern Tree）是一种用于频繁项集挖掘的高效数据结构，其主要应用是改进 Apriori 算法在扫描数据库方面的性能瓶颈。FP 树通过压缩数据集，保留频繁项的共现关系，支持无候选集生成的频繁项挖掘。

核心思想

• 数据压缩：将交易数据转化为树形结构，通过共用前缀压缩存储。
• 递归分解：根据频繁项生成条件模式基，递归挖掘频繁项。
• 关联规则生成：通过频繁项计算支持度、置信度和提升度，生成规则。

算法分析与设计

FP 树构建

• 输入：数据集、最小支持度阈值
• 具体步骤：
  • 计算每个项的支持度，结果保存。不满足设定的最小支持度的删去
  • 根据支持度排序（降序），作为辅助的表保存
  • 根据从大到小的顺序，从根节点按顺序插入 FP 树中。插入的具体操作是如果已经存在该节点就计数加 1，否则就在上个节点分叉。这样做能够表示从任意一个节点到根的路径都是一个数据项，该节点的 value 就是出现的个数（排序保证唯一性了）
• 分析：构建的复杂度是数据集的每个商品的总数

条件 FP 树的生成

上面已经提到，如果沿着树从下向上走，走过的路径就是其中的一个项集（交易）。整棵树又是根据支持度排序之后构建的。那么我们如果知道一个频繁项集中最小支持度的那一个项是什么，然后能够找到所有那个项在树中的节点位置的话，就能找到所有含该项的项集，而且每一个项集（对应路径）出现的次数（支持度）就是我们找到的那个节点上的 value。

我们通过存储每个项对应的所有节点，就能够在 FP 树上恢复出含有该项的所有项集和对应支持度。知道这个就能够再一次构建 FP 树，这次构建的树不含有我们选出的那一项。

本质上就是拆分子问题。FPTree 的 freq_one_item 的表能够帮我们整理在已知数据集下的符合标准的频繁单个项。根据树的结构能够高效的找出含有这个项的项集。那么问题就拆分为找到平凡项集中的一项和其他项。其他项就递归下去查找。因为子问题的时间复杂度不会超过 $O(nlgn)$ （排序，线性扫描，而不是 Apriori 的求幂集），子问题的分解非常快（支持度筛选了），所以非常高效

关联规则的生成

根据上面的生成的平凡项集，这里仍然采用 $O(2^n)$ 的求幂集暴力算法。每次查询支持度因为已经保存了字典了，所以查询这个操作是常数复杂度，整体的时间代价是可以接受的

具体步骤：

1. 枚举每个频繁项的所有非空子集作为规则前件
2. 计算支持度，置信度，提升度
3. 筛选合格的

测试结果

程序正确性

根据书本的数据，有测试程序：

from main import *
 
def test_get_every_single_support():
    data = read_data('book.csv')
    support = get_every_single_support(data)
    assert support["薯片"] == 7
    assert support["鸡蛋"] == 7
 
 
def test_get_PFTree():
    data = read_data('book.csv')
    tree = FPTree(data, min_support=3)
    assert tree.root.children[0].name == "薯片"
    assert tree.root.children[0].value == 7
    assert tree.m_freq_one_item == ["薯片", "鸡蛋", "面包", "牛奶", "啤酒"]
 
 
def test_get_freq_mode():
    data = read_data('book.csv')
    freq_mode = FPTree(data, min_support=3).get_freq_mode()
    assert freq_mode.get("薯片") == 7
    assert freq_mode.get("薯片,鸡蛋") == 6

> pytest                           
=============== test session starts ================
platform win32 -- Python 3.12.3, pytest-8.3.3, pluggy-1.5.0
rootdir: E:\algo\FP_tree
collected 3 items

test_main.py ...                              [100%]

================ 3 passed in 0.03s ================= 

数据分析

对数据集 data.csv 进行测试（100 项，平均长度为 7）

结果如下：

── 啤酒
│   ├── 面包
│   ├── 袜子
│   │   └── 面包
│   │       └── 香皂
│   ├── 牛奶
│   └── 香皂
├── 苹果
├── 尿不湿
│   ├── 苹果
│   ├── 啤酒
│   │   └── 苹果
│   │       └── 香皂
...
洗发露: 59
香蕉: 54
尿不湿: 53
饮料: 53
剃须刀: 51
啤酒: 50
牛奶: 48
袜子: 48
苹果: 46
面包: 44
...
洗发露,饮料,剃须刀,啤酒,牛奶,袜子 => 尿不湿,苹果,香蕉 (Support: 5, Confidence: 2.50, Lift: 1.53)
洗发露,饮料,剃须刀,啤酒,牛奶,袜子 => 苹果,香蕉 (Support: 7, Confidence: 3.50, Lift: 1.33)
香蕉,袜子,苹果,面包 => 饮料,尿不湿,洗发露,剃须刀,啤酒 (Support: 5, Confidence: 0.33, Lift: 1.22)
洗发露,饮料,尿不湿,剃须刀,啤酒 => 袜子,苹果,香蕉,面包 (Support: 5, Confidence: 1.67, Lift: 1.22)
香蕉,剃须刀,啤酒,牛奶,袜子 => 尿不湿,香皂,苹果,饮料 (Support: 3, Confidence: 1.00, Lift: 1.22)
...

分析时间在 1 秒内

对于大测试样例 INTEGRATED-DATASET.csv （1420 项，平均长度为 4）

============================= test session starts =============================
platform win32 -- Python 3.12.3, pytest-8.3.3, pluggy-1.5.0
rootdir: e:\algo\FP_tree
collected 1 item

test_main.py .                                                           [100%]

============================== 1 passed in 1.65s ==============================

耗时为 1.65s

分析与探讨

分析与探讨

1. 实验结论
   • FP 树有效压缩了数据，尤其在数据重复度较高的情况下，构建树结构的效率明显优于直接枚举。
   • 关联规则生成展示了商品间的潜在联系，可用于推荐系统和市场分析。
2. 性能瓶颈
   • 数据规模较大时，条件 FP 树的递归生成可能导致内存消耗较高。
   • 高维数据中，频繁项集的数量急剧增长，关联规则生成可能出现组合爆炸。
3. 改进建议
   • 并行化处理：利用多线程或分布式计算加速 FP 树构建与规则生成。
   • 降维策略：通过领域知识筛选高价值特征，减少频繁项集规模。
   • 优化数据结构：使用更紧凑的数据结构，如稀疏矩阵，进一步压缩条件模式基。

附录：源代码

全部见 https://github.com/Satar07/FP_tree

from anytree import LightNodeMixin, RenderTree
from collections import defaultdict
from itertools import combinations
 
 
class ItemWithSupport:
    def __init__(self, name: str, support: int):
        self.name = name
        self.support = support
 
    def __str__(self):
        return f"{self.name}: {self.support}"
 
 
def read_data(file: str) -> list[list[ItemWithSupport]]:
    data = []
    with open(file, 'r', encoding="utf-8") as f:
        for line in f:
            if line[-2] == ',':
                line = line[:-2]  # Remove extra comma at the end of line
            data.append([ItemWithSupport(s, 1)
                         for s in line.strip().split(',')])
    return data
 
 
def get_every_single_support(data: list[list[ItemWithSupport]]) -> dict[str, int]:
    """Get the support count for every single item in the dataset"""
    support = defaultdict(int)
    for row in data:
        for item in row:
            support[item.name] += item.support
    return dict(support)
 
 
class FPNode(LightNodeMixin):
    __slots__ = ["name", "value"]
 
    def __init__(self, name, value, parent=None, children=None):
        super().__init__()
        self.name = name
        self.value = value
        self.parent = parent
        self.children = children if children is not None else []  # Ensure it's always a list
 
 
class FPTree:
    def __init__(self, data: list[list[ItemWithSupport]], min_support: int):
        self.m_item_to_node = defaultdict(list)
        self.m_min_support = min_support
        self.m_item_support = get_every_single_support(data)
        self.m_freq_one_item = [
            item for item in self.m_item_support if self.m_item_support[item] >= min_support]
        self.m_freq_one_item.sort(
            key=lambda x: self.m_item_support[x], reverse=True)
        self.root = FPNode("root", 0)
 
        sorted_data = []
        for row in data:
            sorted_row = sorted(
                [item for item in row if item.name in self.m_freq_one_item],
                key=lambda x: self.m_item_support[x.name],
                reverse=True
            )
            sorted_data.append(sorted_row)
 
        for row in sorted_data:
            self.insert(row, self.root)
        self.m_freq_mode = self.get_freq_mode()
 
    def insert(self, items: list[ItemWithSupport], node: FPNode):
        """Inserts a list of items into the FP tree"""
        if not items:
            return
        child_node = next(
            (child for child in node.children if child.name == items[0].name), None)
        if child_node:
            child_node.value += items[0].support
            self.insert(items[1:], child_node)
        else:
            new_node = FPNode(items[0].name, items[0].support, parent=node)
            self.m_item_to_node[items[0].name].append(new_node)
            self.insert(items[1:], new_node)
 
    def get_conditional_tree(self, item: str) -> 'FPTree':
        """Get the conditional tree for a given item"""
        data = []
        for node in self.m_item_to_node[item]:
            path = []
            first_support = node.value
            parent = node.parent
            while parent.name != "root":
                path.append(ItemWithSupport(parent.name, first_support))
                parent = parent.parent
            if path:
                data.append(path[::-1])  # Reverse path order
        return FPTree(data, self.m_min_support)
 
    def get_freq_mode(self) -> dict[str, int]:
        """Get the frequent mode of the dataset"""
        freq_mode = {}
        for item in self.m_freq_one_item[::-1]:
            freq_mode[item] = self.m_item_support[item]
            con_tree = self.get_conditional_tree(item)
            sub_freq_mode = con_tree.get_freq_mode()
            for sub_item, sub_support in sub_freq_mode.items():
                combined_item = sub_item + ',' + item
                combined_item_list = combined_item.split(',')
                combined_item_list.sort(
                    key=lambda x: self.m_item_support[x], reverse=True)
                combined_item = ','.join(combined_item_list)
                freq_mode[combined_item] = sub_support
        return freq_mode
 
 
class AssociationRule:
    def __init__(self, antecedent, consequent, support, confidence, lift):
        self.antecedent = antecedent
        self.consequent = consequent
        self.support = support
        self.confidence = confidence
        self.lift = lift
 
    def __str__(self):
        return f"{self.antecedent} => {self.consequent} (Support: {self.support}, Confidence: {self.confidence:.2f}, Lift: {self.lift:.2f})"
 
 
class FPTreeWithRules(FPTree):
    def __init__(self, data: list[list[ItemWithSupport]], min_support: int):
        super().__init__(data, min_support)
 
    def get_support(self, itemset: list[str]) -> int:
        """Calculates the support of a given itemset"""
        sorted_itemset = sorted(
            itemset, key=lambda x: self.m_item_support[x], reverse=True)
        itemset_str = ','.join(sorted_itemset)
        return self.m_freq_mode.get(itemset_str, 0)
 
    def generate_association_rules(self, min_confidence: float, min_lift: float) -> list[AssociationRule]:
        """Generate association rules from the frequent itemsets"""
        rules = []
        freq_itemsets = self.get_freq_mode()
 
        for itemset_str, support in freq_itemsets.items():
            itemset = itemset_str.split(',')
 
            # Generate all possible non-empty subsets of the itemset
            for size in range(1, len(itemset)):
                for antecedent in combinations(itemset, size):
                    antecedent = list(antecedent)
                    consequent = list(set(itemset) - set(antecedent))
 
                    # Calculate support for antecedent and consequent
                    antecedent_support = self.get_support(antecedent)
                    consequent_support = self.get_support(consequent)
 
                    # Calculate confidence and lift
                    if antecedent_support > 0:
                        confidence = support / antecedent_support
                    else:
                        confidence = 0
 
                    if consequent_support > 0:
                        lift = confidence / \
                            (consequent_support / len(self.m_item_support))
                    else:
                        lift = 0
 
                    # Only consider rules with sufficient confidence and lift
                    if confidence >= min_confidence and lift >= min_lift:
                        rule = AssociationRule(
                            antecedent=','.join(antecedent),
                            consequent=','.join(consequent),
                            support=support,
                            confidence=confidence,
                            lift=lift
                        )
                        rules.append(rule)
 
        return rules
 
 
# Example usage
if __name__ == "__main__":
    # Assume that 'data.csv' is the input dataset
    data = read_data('INTEGRATED-DATASET.csv')
    min_support = 2  # Minimum support count
    min_confidence = 0.2  # Minimum confidence threshold
    min_lift = 1  # Minimum lift threshold
 
    tree = FPTreeWithRules(data, min_support)
    print(RenderTree(tree.root).by_attr())
    freq_mode = tree.m_freq_mode
    # top 10 the most frequent itemsets
    for itemset, support in sorted(freq_mode.items(), key=lambda x: x[1], reverse=True)[:10]:
        print(f"{itemset}: {support}")
    rules = tree.generate_association_rules(min_confidence, min_lift)
 
    rules.sort(key=lambda x: x.lift, reverse=True)
    for rule in rules[:10]:
        print(rule)