路由算法

数学抽象

抽象成有权图的形式。这个权重可以是延迟，带宽，实际流量。点是路由器，边是链路。

尝试去对每个路由器，找到到每个点的最短路径（最小开销路径），并根这个得到转发的路由表

信息的获取

• 全局的：所有路由器都有完整的图的信息。可以获得最优解 → 链路状态算法
• 分布式的：路由器只能直接知道相邻的边的信息。需要反复交换信息。

静态&动态

路由变化很慢的时候，可以人工设置。动态则是目前互联网采用的

链路状态选路算法 LS

所有节点都要知道网络拓扑结构：通过把自己知道的信息广播出去，传递到每个节点上，这样就知道了完整的图的信息。通过 Dijkstra 算法 得到到每个点的最短路径，再根据这个计算路由表

可能产生震荡，复杂性较高

距离向量选路算法 DV

bellman-ford方程

定义 $d_x(y)$ 是从 x 到 y 的具有最低开销路径的开销值

有转移方程：

$$d_x(y)=mi{n}_v\{c(x,v)+d_v(y)\}$$

这样，每个节点仅仅将自己所知道的最短路径距离信息告诉邻居

路由器只知道自己直接相连的邻居的距离。当结点从它的任何一个邻居收到一个新的距离向量估值的时候，就使用 BF 方程更新自己的距离向量估值。网络结构不变的情况下，经过一段时间就会稳定，所有路由器的路由表都收敛为最短路径。

好消息传的快，坏消息传得慢：计数到无穷问题

---

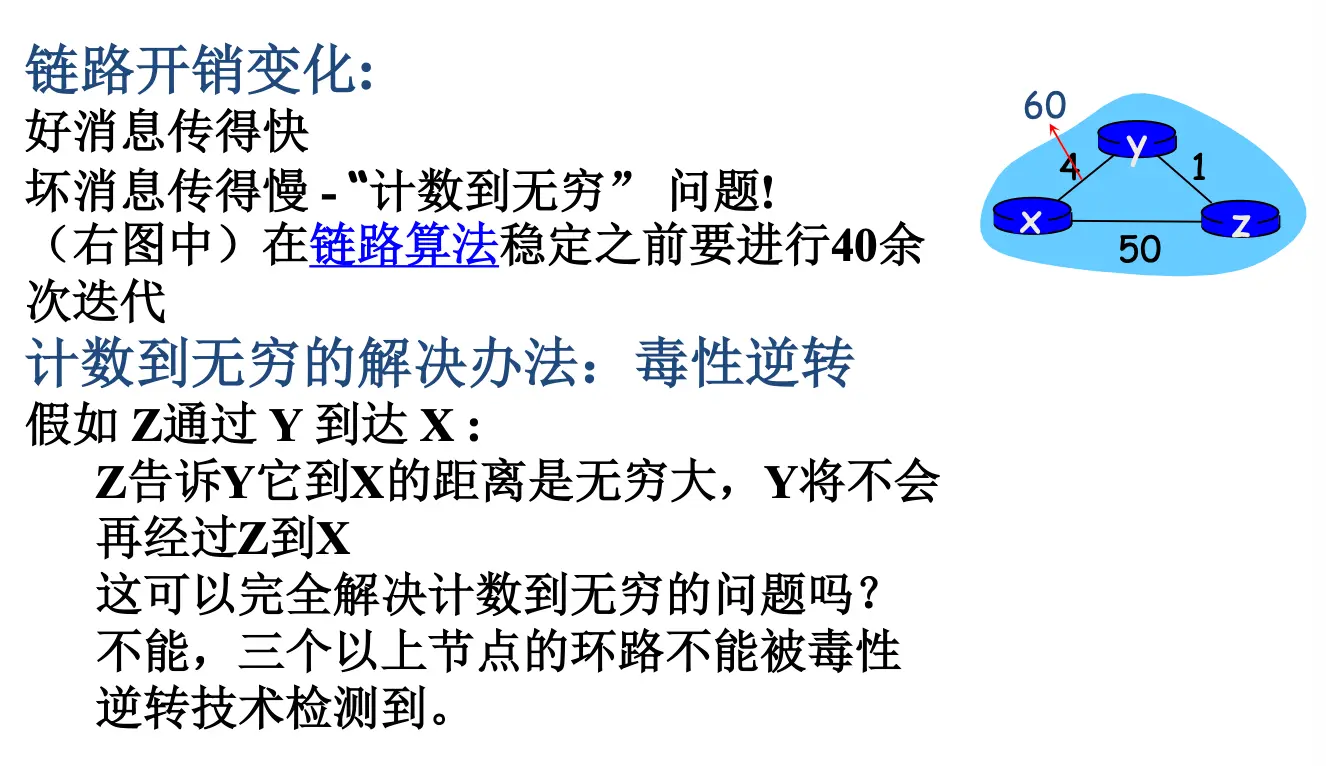
1. 报文复杂性

• LS 算法：
  • 在网络中有 ( n ) 个节点、( E ) 条链路时，每个节点需要向全网广播链路状态信息（LSA）。
  • 报文复杂度为 ( O(nE) )，因为每个链路状态变化需被所有节点感知。
  • 例如：若网络规模增大（如节点数或链路数增加），报文数量会显著上升。
• DV 算法：
  • 仅与直接邻居交换路由信息（距离向量），报文仅在相邻节点间传递。
  • 报文复杂度较低，但收敛时间不固定，可能因网络拓扑变化而波动。

核心区别： LS 的报文复杂度与网络规模正相关，而 DV 的报文开销更小，但信息更新可能滞后。

---

2. 健壮性

• LS 算法：
  • 优点：
    • 节点独立计算最短路径（如 Dijkstra 算法），仅依赖本地链路状态数据库。
    • 若某节点广播错误链路开销，影响范围有限（其他节点可基于全局信息修正）。
  • 缺点：
    • 错误链路信息可能导致局部路径计算错误，但不会全网扩散。
• DV 算法：
  • 缺点：
    • 节点间传递的是“距离向量”（到其他节点的路径开销），错误信息会通过邻居逐步扩散到全网。
    • 例如：若某节点误报路径开销，可能导致全网路由表错误（如“计数到无限”问题）。
  • 优点：
    • 邻居间直接交换信息，对局部故障有一定容错性（如 RIP 协议）。

核心区别： LS 的健壮性更强，因错误影响局部化；DV 的健壮性较差，错误可能全网传播。

---

3. 收敛速度

• LS 算法：
  • 收敛时间为 ( O(n^2) )（Dijkstra 算法复杂度），在网络稳定时快速收敛。
  • 潜在问题：频繁链路状态变化可能导致路由振荡（如负载敏感场景）。
• DV 算法：
  • 收敛时间不固定，依赖邻居间迭代更新。
  • 典型问题：
    • 循环路由：因路径信息传播延迟，可能出现路由环路。
    • 计数到无限：错误路径开销被反复放大，导致路由表无法收敛。

核心区别： LS 收敛速度更快且稳定（适合动态网络），而 DV 可能因环路或错误传播导致收敛延迟。