假设检验

• 对这个指标是什么类型做出预判：非参数假设检验
• 判断分布之后，判断参数是否符合标准：非参数假设检验

小概率事件原理

一个概率很小的随机事件，做一次实验，我们认为它是不会发生的

指向原始笔记的链接

先假设，再检验

• 原假设：$H_0$ （选择能够计算的）
• 对立假设：$H_1$

当 $H_0$ 成立时 ，得到一个变量的分布（构建检验统计量），从而得到在抽样下该事件发生的概率。根据小概率事件原理，得到发生和不发生之间的矛盾，进而推翻了 $H_0$ 假设，从而证明了 $H_1$ 成立

1. 确定原假设和对立假设
2. 确定假设统计量（和枢轴变量同理）
3. 确定拒绝域（确定显著性水平）
4. 决策

---

1. 设 $H_0$：融化点是 1260；$H_1$：不是 1260
2. 检验统计量是 $\mu$：根据 第四结论，计算得到具体的值 T，当 $H_0$ 成立时，它服从 $t(n-1)$ 分布
3. 构造一个和目标相关的小概率事件：$P\left\{|\frac{\bar{X}-\mu }{s/\sqrt{n}}|\ge t_{\alpha /2}(n-1)\right\}=\alpha$ （这个小概率事件发生的话能够推翻原假设）这个事件称为 拒绝域（相反为 接受域）

这里需要取绝对值，因为不取的话只取一边，这个事件发生的时候可能不能说明 $H_0$ 发生（均值很大或者很小），从而不能完成下面的推理了

---

假设检验的两类错误

第一类错误：弃真

$$P\{\text{拒绝}{H}_0\mid H_0\text{正确}\}=\alpha$$

就是显著性水平，说明 $\alpha$ 给定越小，发生弃真的情况越小

第二类错误：纳伪

$$P\{\text{接受}{H}_0\mid H_0\text{错误}\}=\beta$$

$\beta$ 是特定状况下能够计算的量（$H_1$ 下的分布情况是已知的，如已知 $\mu$ 真实值）

需要转化为在 $H_1$ 下的枢轴变量，同时保证不等式不发生变化来计算这个事件的概率

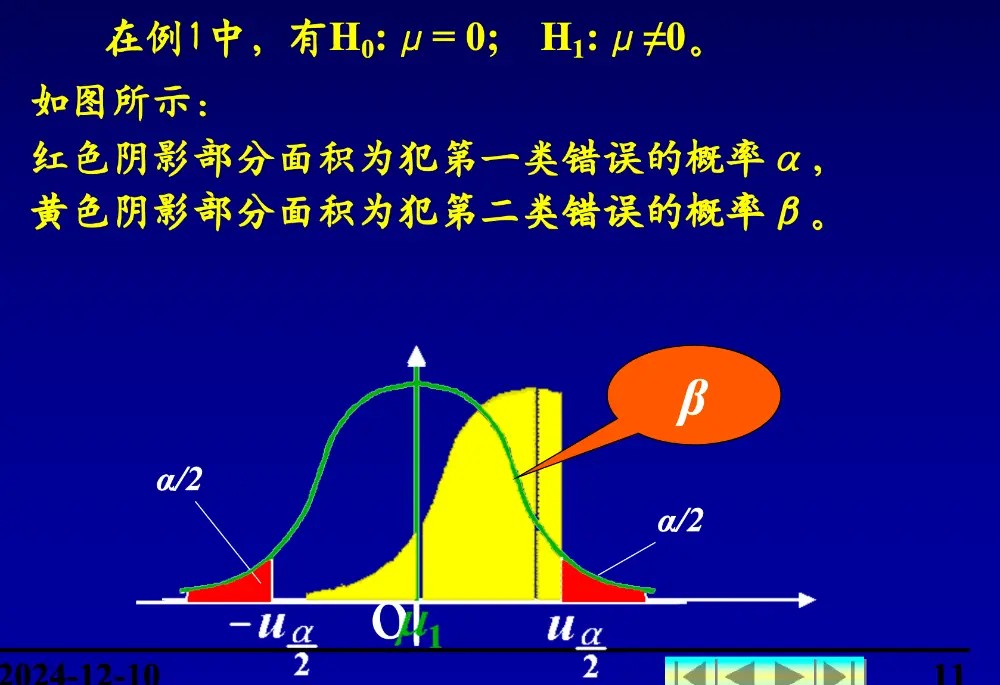
奈曼—皮尔逊 (Neyman-Pearson) 原则：先控制犯第一类错误的概率 $\alpha$，然后再使犯第二类错误的概率 $\beta$ 尽可能地小

以上面的例子来说，就是先保证显著性水平足够小，再让黄色的区间对应的钟型曲线经可能右移，也就是让 n 增大

---

参数的假设检验

大样本的假设检验方法