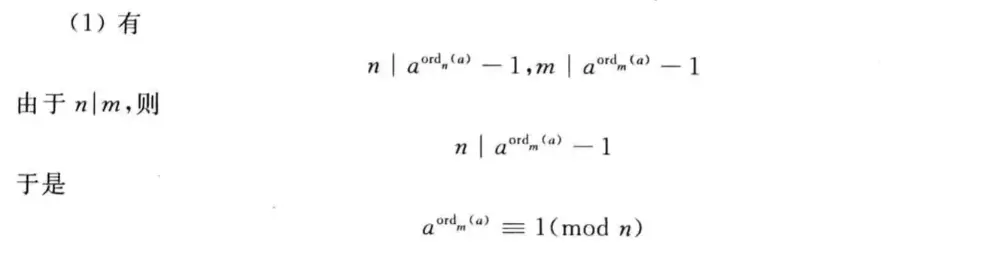元素的阶
如果 a≡b(modm)
ordm(a)=ordm(b)
ad≡1(modm) 的充要条件是
ordm(a)∣d
ordm(a)∣φ(m)
ordm(a−1)=ordm(a)
即元素的阶等于它逆元的阶
证明用阶的定义和互相整除得到
a0,a1,…,aordm(a)−1
两两不同余,特别的当 a 为原根,这 φ(m) 个数构成模 m 简化剩余系
ad≡ak(modm)⟹d≡k(modordm(a))
证明:
ad−k≡1(modm)⟹ordm(m)∣d−k
设 k 为非负整数
ordm(ak)=(ordm(a),k)ordm(a)
而且在模 m 的简化剩余系中,至少有 φ(ordm(a)) 个数对模 m 的指数等于 ordm(a)
这里的至少只计算了由 a 生成的小循环群中和 a 相同阶的情况,没有计算其他循环群的情况
循环群阶的计算
如果 a 是原根,则 ak 是原根的充分必要条件是
(φ(m),k)=1
如果模 m 存在一个原根,则模 m 有 φ(φ(m)) 个不同的原根
ordm(ab)=ordm(a)ordm(b)⟺(ordm(a),ordm(b))=1
用阶的“最小性”定义来说明
ad≡1(modm1m2)
若在 ai≡1(modm1m2) 的情况下能证明 d∣i 总成立,那么说明 d 就是 a 的阶

n∣m⟹ordn(a)∣ordm(a)
(n,m)=1⟹ordnm(a)=[ordn(a),ordm(a)]
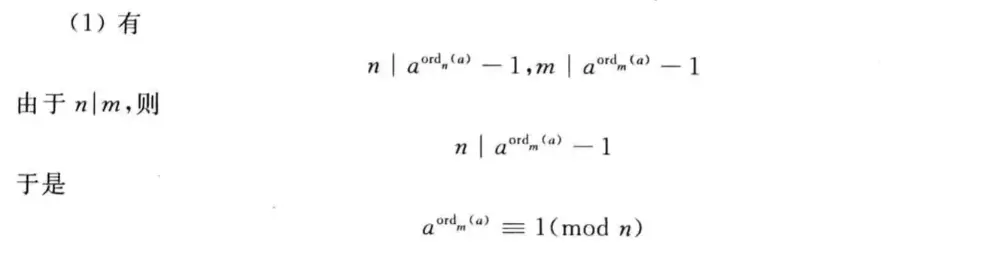


根据 中国剩余定理 有唯一解
有
{ordm1(a)=ordm1(a1)ordm2(a)=ordm2(a2)
则根据上面的定理可以得出