对 弧长微元 做积分即可得到弧长长度
s=\int _{a}^{b} \, ds=\int_{a}^{b} \sqrt{ 1+y' ^{2}}dx空间曲线也是一样的
在极坐标下
设:
则有
定理 函数在曲线上连续,同时知道参数方程且具有一阶导数,则积分可以表示成:
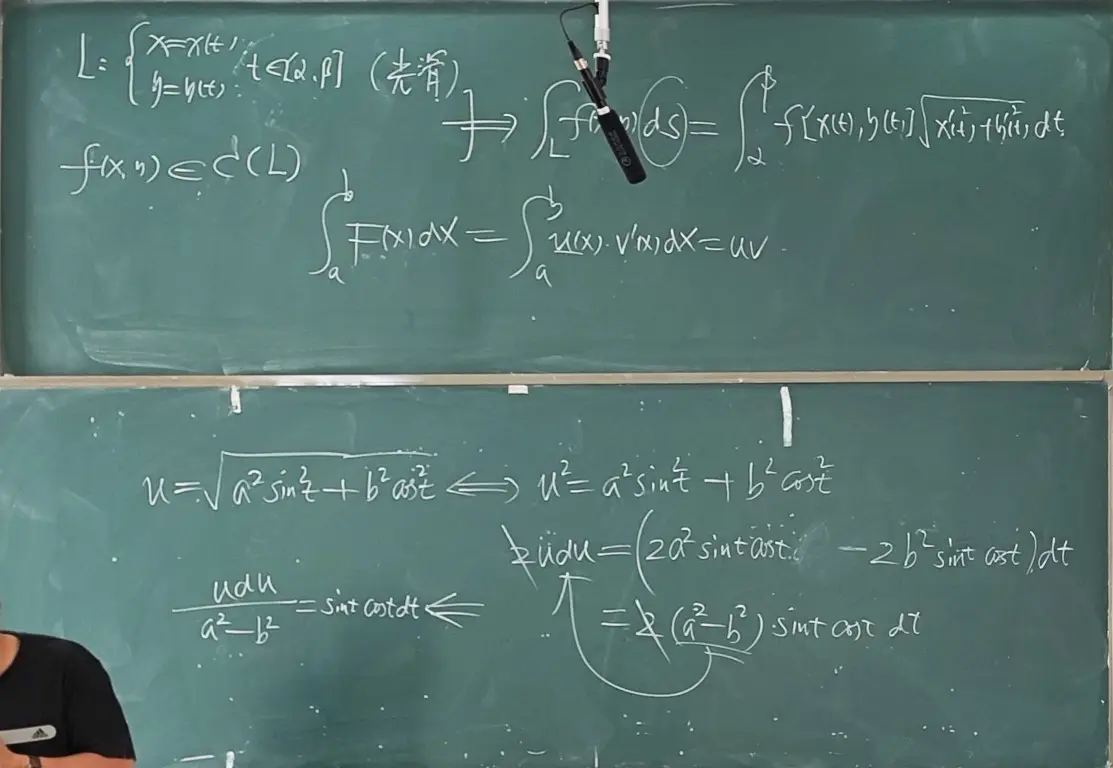
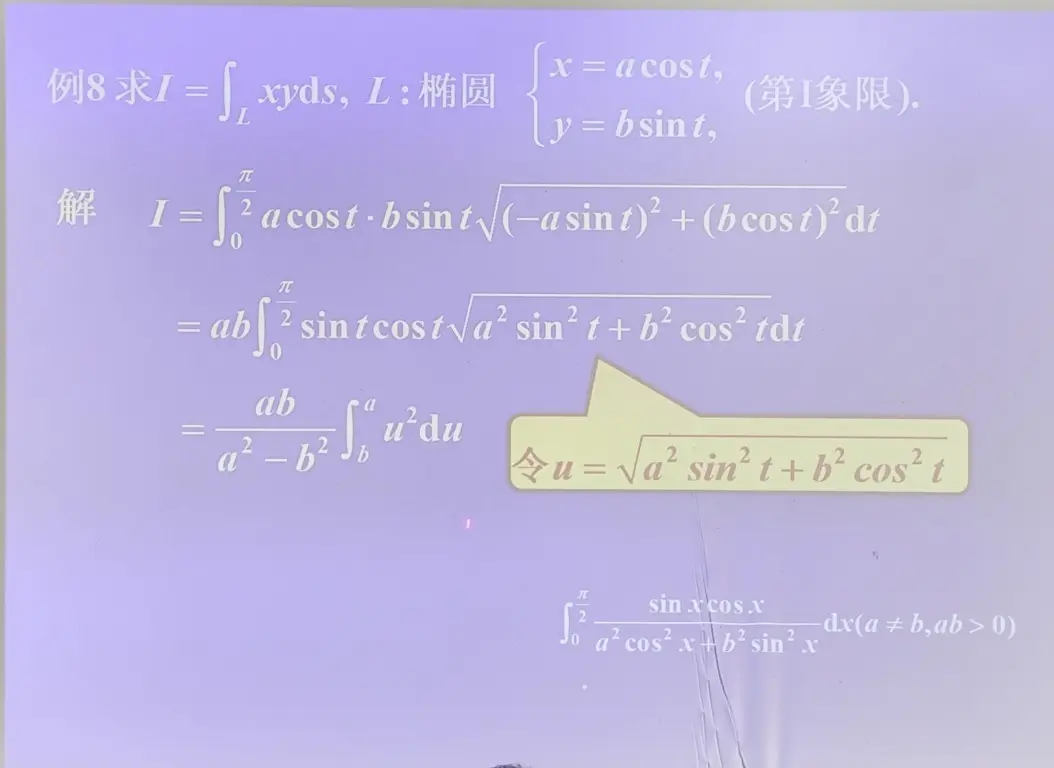
技巧:积分区域的轮换可以帮助计算
部分的奇函数可以拿掉
对 弧长微元 做积分即可得到弧长长度
s=\int _{a}^{b} \, ds=\int_{a}^{b} \sqrt{ 1+y' ^{2}}dx空间曲线也是一样的
在极坐标下
设:
则有
定理 函数在曲线上连续,同时知道参数方程且具有一阶导数,则积分可以表示成:
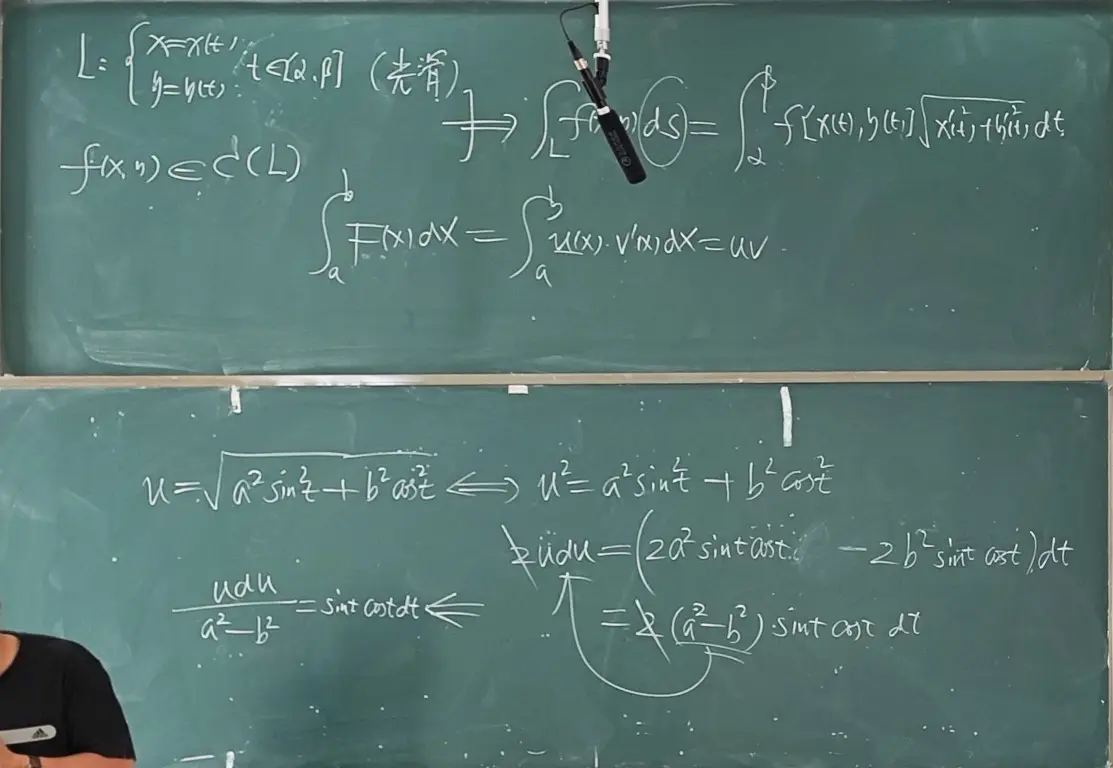
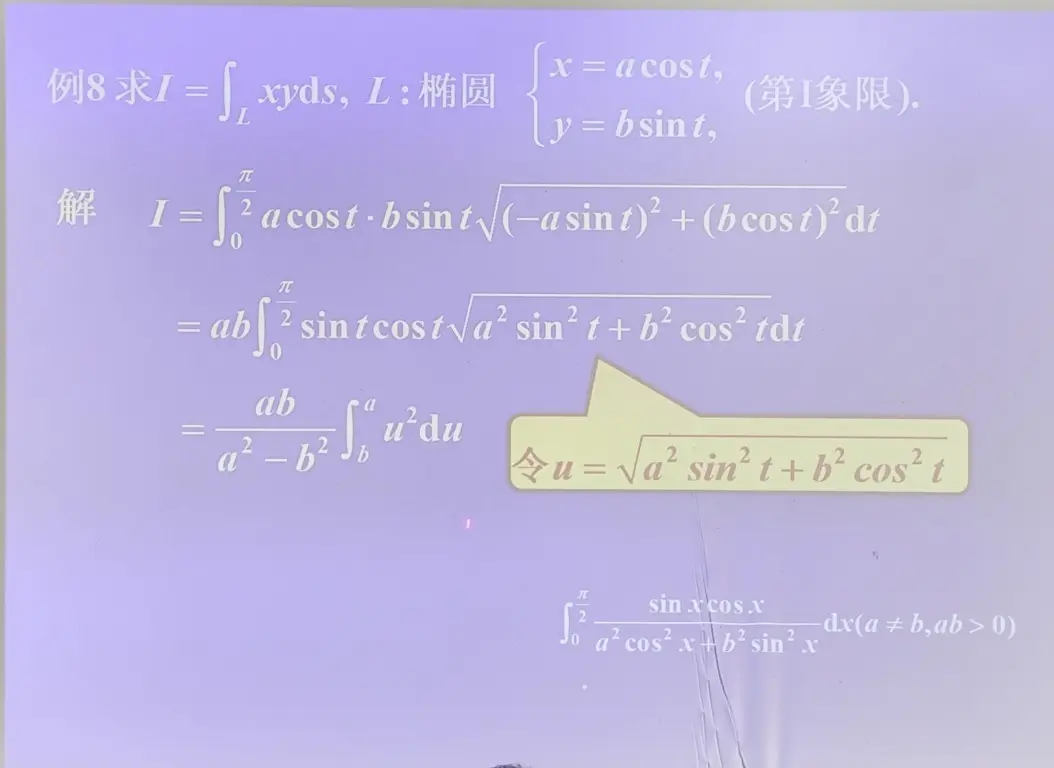
技巧:积分区域的轮换可以帮助计算
部分的奇函数可以拿掉