信息率失真函数

想象一下发微信，你发了一个“你好”，结果他收到了“你坏”，这就是失真。在信息论里，我们希望能够量化这种失真（评估失真程度），并且找到最小化失真的方法。

对于每一对发送符号 $a_i$ 和接收符号 $b_j$，我们定义一个非负函数 $d(a_i,b_j)$ 量化发送 a 接收 b 所产生的错误或不匹配的“程度”

• 汉明失真：如果不等就等于 1，只关心是否出错，不关心错的多离谱
• 平方误差失真：常用于连续信号，就是两个数相减平方

将失真度表示成矩阵形式：失真矩阵

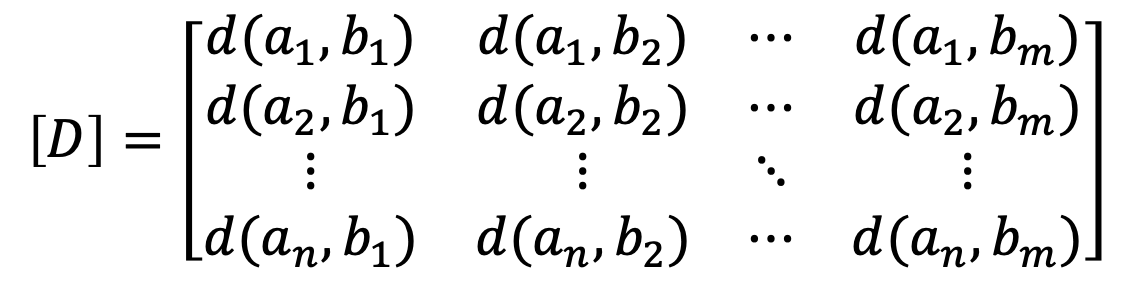
好的，我们来深入理解一下“信息率失真函数”的定义。这可是信息论中非常精髓的一个概念，尤其在数据压缩领域至关重要。

信息率失真函数的定义：

信息率失真函数，通常记为 $R(D)$，它的核心思想是回答这样一个问题：在允许的平均失真度不超过 $D$ 的前提下，我们至少需要多少比特（信息率）来表示信源信息？ 换句话说，它告诉我们为了达到某种可接受的失真水平，信息被压缩的极限是多少。

信息率失真函数 $R(D)$ 定义为：在给定信源 $X$（概率分布 $p(a_i)$）和失真函数 $d(a_i,b_j)$ 的情况下，在所有使得平均失真度 $\bar{D}$ 不超过允许失真度 $D$ 的假想信道 $p(b_j/a_i)$ 中，平均互信息量 $I(X;Y)$ 的最小值。

$$R(D)=\underset{p(b_j/a_i):\bar{D}\le D}{\min }I(X;Y)$$

其中，平均失真度 $\bar{D}$ 的计算公式为：

$$\bar{D}=\sum _{i=1}^n\sum _{j=1}^{m}p(a_i)p(b_j/a_i)d(a_i,b_j)$$

这里 $P_D$ 被称为 D 失真许可的试验信道。

为什么是“最小互信息量”？

理解这一点很关键：

• 互信息量 $I(X;Y)$ 衡量的是接收端 $Y$ 关于发送端 $X$ 获得了多少信息。简单来说，它表示了信源 $X$ 和接收信号 $Y$ 之间的统计依赖程度，或者说 $Y$ 减少了多少关于 $X$ 的不确定性。
• 在数据压缩中，我们希望尽可能少地传输信息（即压缩率高），同时又满足对失真的要求。
• 将“信源编码器”看作是一个“假想信道”。我们通过调整这个“假想信道”的转移概率 $p(b_j/a_i)$，来模拟编码和解码过程。
• 当我们寻找在给定失真 $D$ 下的最小信息率时，我们实际上是在寻找一种“最佳”的编码策略。这种策略应该在满足失真要求的同时，传输最少的信息。而传输最少的信息，等价于信源和接收端之间的互信息量最小化，因为我们希望只传输那些能达到 $D$ 失真所必需的信息，而不是多余的信息。
• 从数学角度讲，互信息量 $I(X;Y)$ 是关于转移概率 $p(b_j/a_i)$ 的下凸函数，因此存在最小值

形象理解：

你可以把 $R(D)$ 想象成一个“价格表”：

• $D$ 是你愿意接受的“质量损失”程度（比如图像模糊一点，声音不那么清晰）。
• $R(D)$ 是你需要为这种“质量损失”付出的“信息代价”——你至少需要传输多少比特才能达到这种质量。
• $R(D)$ 曲线会随着 $D$ 的增加而单调递减。这意味着，如果你允许更大的失真，你所需的信息率就会越小，也就是可以压缩得更厉害。
• 当 $D=0$ 时（不允许任何失真），$R(0)=H(X)$。这意味着如果要完全无损地传输信源信息，所需的信息率就是信源的熵 $H(X)$，这是信源的固有不确定性。
• 当 $D$ 达到某个最大可允许失真 $D_{max}$ 时，$R(D_{max})=0$。这表示在可以接受最大失真时，甚至不需要传输任何信息，因为接收端可以直接猜测或者默认一些值而失真仍在可接受范围内。

R(D) 函数的性质：

1. 定义域：$D$ 的取值范围是从 $D_{min}$ 到 $D_{max}$。通常 $D_{min}=0$。
2. 下凸性：信息率失真函数 $R(D)$ 是允许平均失真度 $D$ 的下凸函数。这意味着随着 $D$ 增加， $R(D)$ 下降的速度会逐渐减缓，或者说，当 $D$ 达到一定程度后，再增加 $D$ 对降低 $R$ 的帮助就不那么大了。
3. 单调递减和连续性：$R(D)$ 是一个单调递减的函数，并且是连续的。允许的失真越大，所需的信息率就越小。

特性	信道容量 $C$	信息率失真函数 $R(D)$
函数特性	$I(X;Y)$ 的上凸函数	$I(X;Y)$ 的下凸函数
目标	$I(X;Y)$ 的极大值	$I(X;Y)$ 的条件极小值
变量依赖（不变量）	$p(b_j/a_i)$ 的函数 (信道)	$p(a_i)$ 的函数 (信源)
依赖关系	仅与信道特性有关	仅与信源特性有关
解决问题	解决可靠性问题	解决有效性问题 (压缩)
基础	信息传输的基础	信源压缩的基础

$$D_{\min }=\sum _{i}p(a_i)\underset{j}{\min }d(a_i,b_j)$$ $$D_{\max }=\underset{j}{\min }\sum _{i}p(a_i)d(a_i,b_j)$$

离散信源信息率失真函数的参量表达式

对于等概率 $m$- 元信源、汉明失真，失真函数为（以自然对数）：

$$R(D)=\ln m-H_m(D)\text{其中 }{H}_m(D)=D\ln (m-1)-D\ln D-(1-D)\ln (1-D)$$

信息价值

限失真信源编码

在允许一定失真的情况下，通过优化编码方式来最大化压缩数据、提高通信效率

对于任意允许的平均失真度 $D\ge 0$，和任意小的 $ϵ>0$，若信息率 $R>R(D)$，只要信源序列 L 足够长，就一定存在一种编码方式 C 使译码之后的平均失真度 $\bar{D}(C)\le D+ϵ$

反之，若 $R<R(D)$ 则必有 $\bar{D}(C)>D$