离散信源信息率失真函数的参量表达式

在信息论中，直接求 $R(D)=\min I(X;Y)$ 往往比较复杂，因为它涉及在满足平均失真约束下对所有可能的转移概率 $p(b_j/a_i)$ 进行优化。为了简化计算，通常会引入一个拉格朗日乘子 $\lambda$（或者这里的 $S$）来构造一个辅助函数，从而通过求偏导的方式找到最小值。

离散信源信息率失真函数的参量表达式，通常是通过引入一个参数 $S$ 来定义的。这个 $S$ 可以看作是一个“斜率”或者“代价因子”，它将互信息量和平均失真度结合起来。

构造拉格朗日辅助函数函数 $I(X;Y)+S\cdot \bar{D}-\mu \left(\sum p(b_j\mid a_i)-1\right)$

$$-\sum _i\sum _{j}p(a_i)p(b_j/a_i){\log }_{2}p(b_j/a_i)-S\sum _i\sum _{j}p(a_i)p(b_j/a_i)d(a_i,b_j)-{\mu }_i\left(\sum _{j}p(b_j\mid a_i)-1\right)$$

对转移概率求偏导之后等于 0，一通化简。在满足给定失真函数 $d(a_i,b_j)$ 和信源概率 $p(a_i)$ 的条件下，能够使平均互信息量最小化的最优试验信道转移概率 $p(b_j/a_i)$ 满足以下形式：

$$p(b_j/a_i)=p(b_j)\cdot 2^{S\cdot d(a_i,b_j)}\cdot {\lambda }_i$$

其中：

• $S$ 是一个参数，通常 $S<0$ 。
• $p(b_j)$ 是接收端符号 $b_j$ 的概率。
• $d(a_i,b_j)$ 是失真函数。
• ${\lambda }_i$ 是一个归一化常数，确保 ${\sum }_{j}p(b_j/a_i)=1$ 对所有 $i$ 都成立。

$$D(S)=\sum _{i=1}^n\sum _{j=1}^{m}p(a_i)p(b_j/a_i)d(a_i,b_j)$$ $$R(S)=S\cdot D(S)+\sum _{i=1}^{n}p(a_i)\ln {\lambda }_i$$

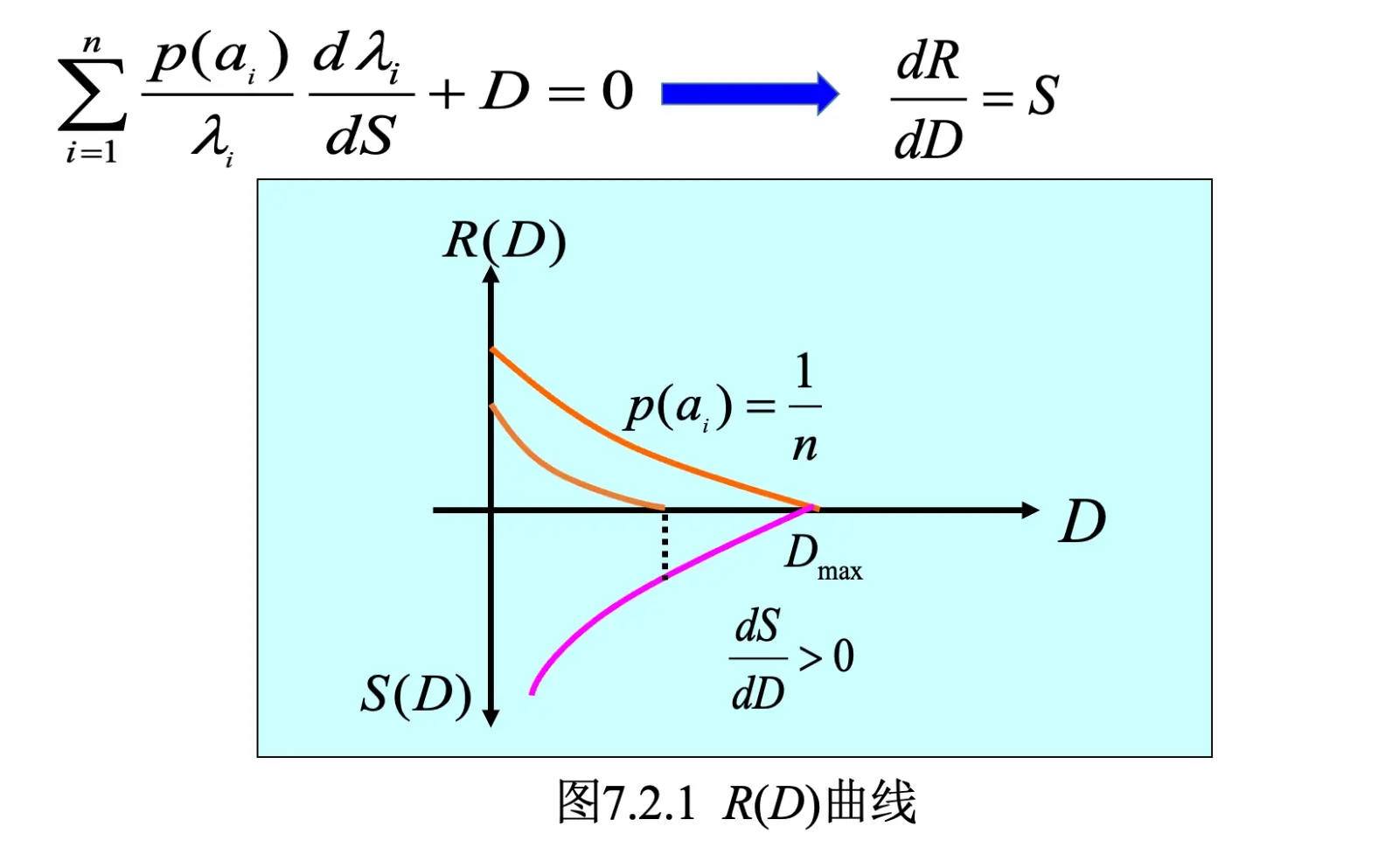
下面紫色的是斜率，也就是 S。反正就记住这个图长这样就行

---

下面是一个计算实例

二元及等概率离散信源的信息率失真函数的计算方法

二元及等概率离散信源的定义

首先，我们明确信源的特性：

• 信源 $X$: 只有两个可能的输出符号，例如 $a_1$ 和 $a_2$。
• 概率分布 $P(X)$: $P(X)=\left[\begin{array}{cc}{a}_1& a_2\\ p& 1-p\end{array}\right]$。
• 等概率信源：意味着 $p=0.5$。当 $p=0.5$ 时，信源熵 $H(X)=-0.5{\log }_{2}0.5-(1-0.5){\log }_2(1-0.5)=1$ 比特。

失真矩阵 $D$

PPT 中给出了失真矩阵 $D=\left[\begin{array}{cc}0& \alpha \\ \alpha & 0\end{array}\right]$，其中 $\alpha >0$。这表示：

• $d(a_1,a_1)=0$：发送 $a_1$ 收到 $a_1$ 没有失真。
• $d(a_2,a_2)=0$：发送 $a_2$ 收到 $a_2$ 没有失真。
• $d(a_1,a_2)=\alpha$：发送 $a_1$ 收到 $a_2$ 产生 $\alpha$ 的失真。
• $d(a_2,a_1)=\alpha$：发送 $a_2$ 收到 $a_1$ 产生 $\alpha$ 的失真。 这是一种对称失真，是汉明失真的一种推广（当 $\alpha =1$ 时就是标准的汉明失真）。

最大允许失真度 $D_{max}$

最大允许失真度 $D_{max}$ 是指在不传输任何信息（即信息率 $R=0$）的情况下，能够达到的最小平均失真度。 $D_{max}={\min }_j{D}_j$，其中 $D_j={\sum }_{i=1}^{n}p(a_i)d(a_i,b_j)$

对于二元信源和上述对称失真：

• 如果接收端总是输出 $b_1$：$D_1=p(a_1)d(a_1,b_1)+p(a_2)d(a_2,b_1)=p\cdot 0+(1-p)\cdot \alpha =(1-p)\alpha$.
• 如果接收端总是输出 $b_2$：$D_2=p(a_1)d(a_1,b_2)+p(a_2)d(a_2,b_2)=p\cdot \alpha +(1-p)\cdot 0=p\alpha$ $D_{max}$ 取 $D_1$ 和 $D_2$ 中的较小值。在二元等概率信源（$p=0.5$）的情况下，$D_1=0.5\alpha$ 且 $D_2=0.5\alpha$，所以 $D_{max}=0.5\alpha$.

计算步骤（参量表达式法）

信息率失真函数的计算通常采用拉格朗日乘子法，引入参数 $S$。

确定最优转移概率 $p(b_j/a_i)$ 的形式

最优的信道转移概率 $p(b_j/a_i)$ 满足以下形式：

$$p(b_j/a_i)={\lambda }_{i}p(b_j)e^{Sd(a_i,b_j)}$$

其中 ${\lambda }_i$ 是归一化常数，确保 ${\sum }_{j}p(b_j/a_i)=1$。

计算 ${\lambda }_i$ 的表达式:

根据归一化条件 ${\sum }_{j}p(b_j/a_i)=1$，我们可以得到：

$$1=\sum _{j=1}^{m}p(b_j/a_i)={\lambda }_i\sum _{j=1}^{m}p(b_j)e^{Sd(a_i,b_j)}$$

所以，$\frac{1}{{\lambda }_i}={\sum }_{j=1}^{m}p(b_j)e^{Sd(a_i,b_j)}$。对于二元信源（$a_1,a_2$）和二元输出（$b_1,b_2$），且失真矩阵如上所示：

• 当 $i=1$ (发送 $a_1$)： $1/{\lambda }_1=p(b_1)e^{Sd(a_1,b_1)}+p(b_2)e^{Sd(a_1,b_2)}=p(b_1)e^{S\cdot 0}+p(b_2)e^{S\alpha }=p(b_1)+p(b_2)e^{S\alpha }$.
• 当 $i=2$ (发送 $a_2$)： $1/{\lambda }_2=p(b_1)e^{Sd(a_2,b_1)}+p(b_2)e^{Sd(a_2,b_2)}=p(b_1)e^{S\alpha }+p(b_2)e^{S\cdot 0}=p(b_1)e^{S\alpha }+p(b_2)$.

计算 $p(b_j)$ 和 $p(b_j/a_i)$ 的表达式

由 $p(b_j)={\sum }_{i}p(a_i)p(b_j/a_i)$，且 $p(b_j/a_i)={\lambda }_{i}p(b_j)e^{Sd(a_i,b_j)}$，代入并简化

• $p(b_1)=\frac{p-(1-p)e^{S\alpha }}{1-e^{2S\alpha }}$.
• $p(b_2)=\frac{(1-p)-p{e}^{S\alpha }}{1-e^{2S\alpha }}$.

将 ${\lambda }_i$ 和 $p(b_j)$ 的表达式代入 $p(b_j/a_i)={\lambda }_{i}p(b_j)e^{Sd(a_i,b_j)}$ 最终得到：

• $p(b_1/a_1)=\frac{p-(1-p)e^{S\alpha }}{p(1-e^{2S\alpha })}$.
• $p(b_2/a_1)=\frac{(1-p)-p{e}^{S\alpha }}{p(1-e^{2S\alpha })}{e}^{S\alpha }$.
• $p(b_1/a_2)=\frac{p-(1-p)e^{S\alpha }}{(1-p)(1-e^{2S\alpha })}{e}^{S\alpha }$.
• $p(b_2/a_2)=\frac{(1-p)-p{e}^{S\alpha }}{(1-p)(1-e^{2S\alpha })}$.

需要注意，这些概率值必须大于等于零，所以存在 $S$ 的取值范围，通常 $e^{S\alpha }\le \min (\frac{p}{1-p},\frac{1-p}{p})$

计算 $D(S)$ (平均失真度) 的参量表达式

$$D(S)=\sum _{i=1}^n\sum _{j=1}^{m}p(a_i)p(b_j/a_i)d(a_i,b_j)$$

将上面得到的 $p(b_j/a_i)$ 代入，经过化简，对于二元信源和对称失真，可以得到：

$$D(S)=\frac{\alpha e^{S\alpha }}{1+e^{S\alpha }}$$

计算 $R(S)$ (信息率) 的参量表达式

$$R(S)=S\cdot D(S)+\sum _{i=1}^{n}p(a_i)\ln {\lambda }_i$$

这里 $\ln$ 是自然对数，如果互信息量用 ${\log }_2$ 表示，则公式需要乘以 $\frac{1}{\ln 2}$。

将 $D(S)$ 和 $\ln {\lambda }_i$ 的具体表达式代入，经过化简，可以得到 $R(S)$：

$$R(S)=\frac{S\alpha e^{S\alpha }}{1+e^{S\alpha }}-p\ln p-(1-p)\ln (1-p)-\ln (1+e^{S\alpha })$$

（注意这里的对数基数通常是 $e$，如果最终结果需要比特，则需转换为 ${\log }_2$）

最终 $R(D)$ 表达式 (当 $p=0.5$ 时)

$$R(D)=H(p)-H\left(\frac{D}{\alpha }\right)$$

其中 $H(p)=-p{\log }_{2}p-(1-p){\log }_2(1-p)$ 是信源熵。$H(x)=-x{\log }_{2}x-(1-x){\log }_2(1-x)$ 是二元熵函数。对于等概率信源，即 $p=0.5$：$H(0.5)=1$ 比特。所以，对于二元等概率信源和对称失真函数，信息率失真函数最终简化为：

$$R(D)=1-H\left(\frac{D}{\alpha }\right)$$

总结

计算二元及等概率离散信源的信息率失真函数，通常涉及以下步骤：

1. 定义信源和失真函数：确定信源符号概率 $p(a_i)$ 和失真矩阵 $d(a_i,b_j)$。对于二元等概率信源，通常 $p(a_1)=p(a_2)=0.5$，失真矩阵是对称的，非对角线元素为 $\alpha$。
2. 引入参数 $S$：通过拉格朗日乘子法，构造一个辅助函数，并对 $S$ 求偏导。
3. 推导最优转移概率 $p(b_j/a_i)$： 这是核心步骤，需要解出一组以 $S$ 和信源参数表示的 $p(b_j/a_i)$。
4. 计算 $D(S)$ 和 $R(S)$ 的参量表达式：将推导出的最优 $p(b_j/a_i)$ 代入平均失真度和互信息量的公式，得到 $D(S)$ 和 $R(S)$ 的表达式。
5. 消除参数 $S$ (如果可能)：通常情况下，可以从 $D(S)$ 的表达式中反解出 $S$ 关于 $D$ 的函数，再代入 $R(S)$，从而得到 $R(D)$ 的显式表达式。对于二元等概率对称失真信源，这个最终形式非常简洁，即 $R(D)=1-H(D/\alpha )$ 。