可微的性质

一元函数可微一定可导，可导一定可微，

多元函数：

连续偏导数未必存在，反过来也未必存在

可微必然连续：多元函数的连续性 定义证明

可微偏导数一定存在：如果当 z 是偏增量，则可以推出偏导数存在

$$f(x,y)=\{\begin{array}{l}\frac{xy}{\sqrt{x^2+y^2}},(x,y)\ne (0,0),\\ 0,(x,y)=(0,0),\end{array}$$

上面的函数 x，y 在（0,0）的偏导数都存在且都等于 0，但是考察高阶无穷小的时候并不是 0

所以偏导数存在推不出可微

连续推不出可微：上面的函数连续但是在零点不可微

连续且偏导数存在也推不出可微：上面的函数就是

NOTE

函数的连续和偏导数都是可微的必要不充分条件

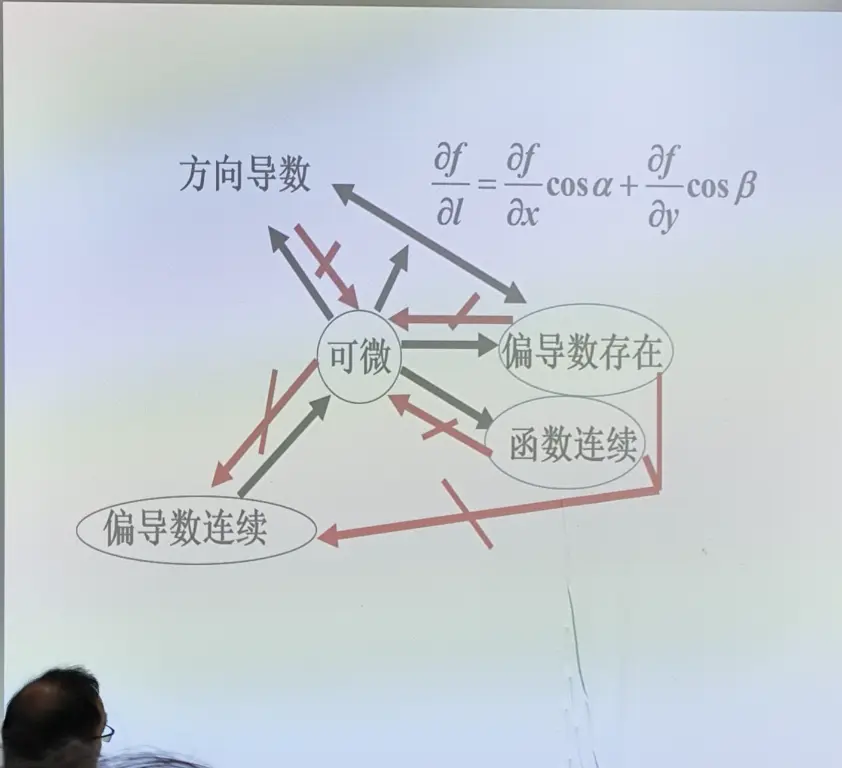
如果偏导函数存在，而且偏导函数连续能不能推出偏导函数可微？

1. 添项，增加一个直角转弯的中间过渡——全增量化为偏增量，二元函数化为一元函数
2. 在一个方向上用拉格朗日中值定理写成线性项（有拉格朗日余项）
3. 利用用偏导数的连续，取极限把导数里面的自变量增量（拉格朗日余项）扔掉，写成偏增量线性项加上一个无穷小量，另一个自变量同理
4. 利用绝对值不等式（和的绝对值小于绝对值的和），放缩，最后小于等于两个无穷小量，利用夹逼准则推出等于 0，推出确实是高阶无穷小

NOTE

如果存在连续偏导函数，则函数可微

能不能减弱偏导函数连续的条件？

可以减弱到一个连续一个存在