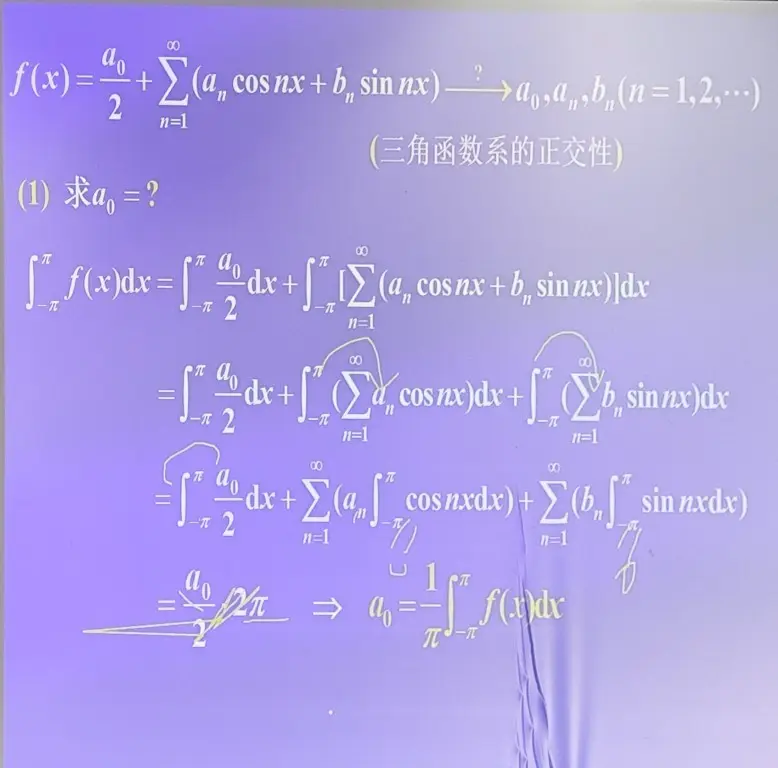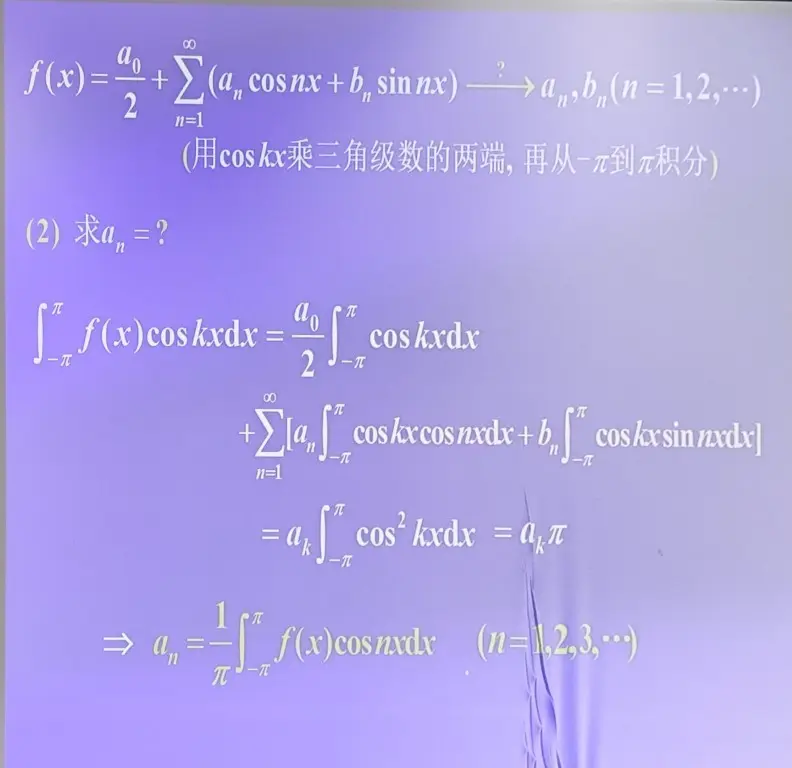设 是以 为周期的函数,且能够展开为三角级数,那么傅里叶级数的系数和原函数的关系是什么呢?
即 求正交基的表出系数(下面图片的方法有点笨了,放最后了)已知:
最后得到:
可以充分利用函数的奇偶性来使式子化简更快:
- f 是奇函数,只剩下 sin 项
- f 是偶函数,只剩下 1 和 cos 项
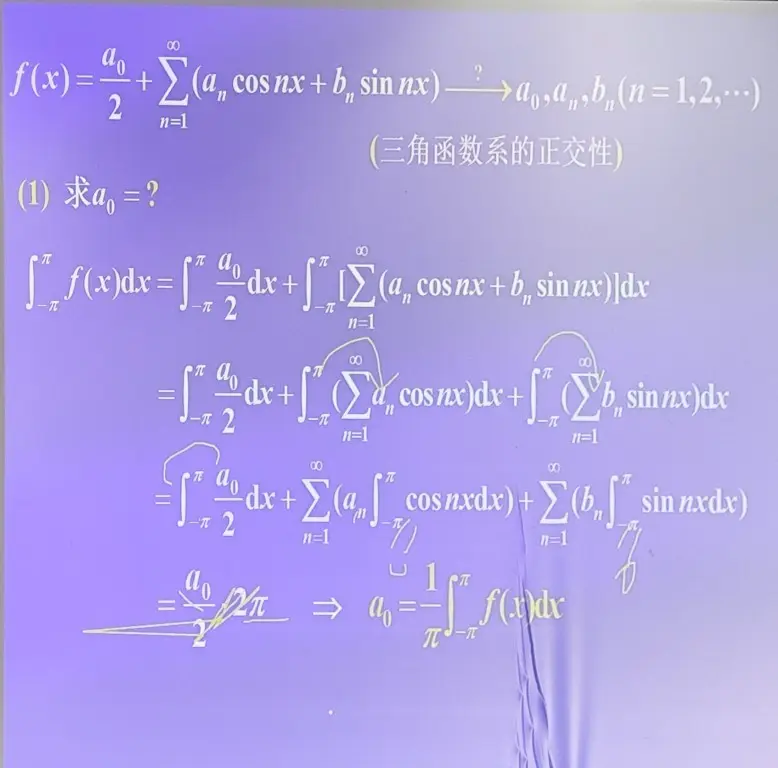
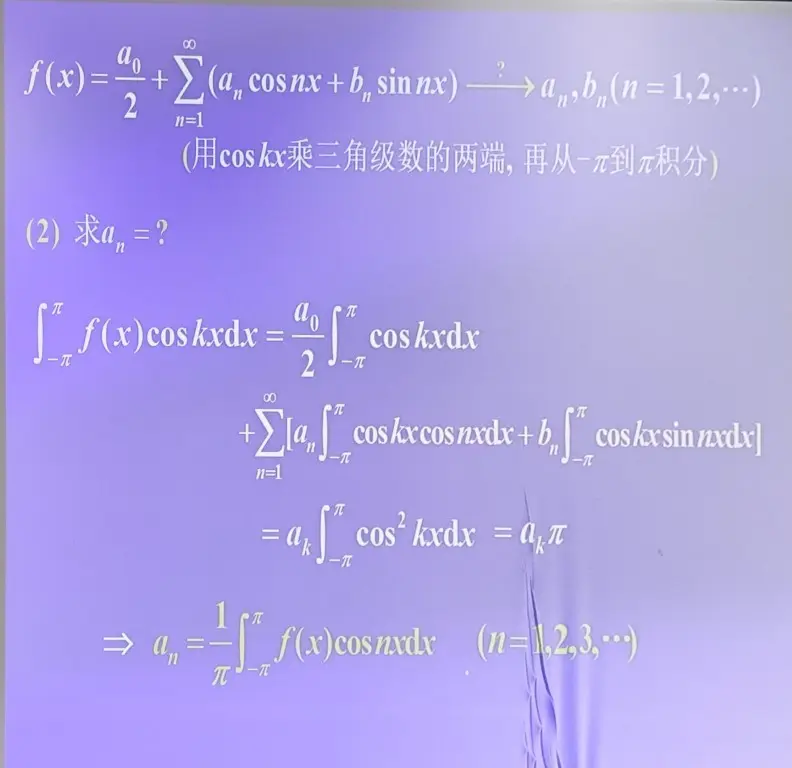

设 是以 为周期的函数,且能够展开为三角级数,那么傅里叶级数的系数和原函数的关系是什么呢?
即 求正交基的表出系数(下面图片的方法有点笨了,放最后了)已知:
最后得到:
可以充分利用函数的奇偶性来使式子化简更快: