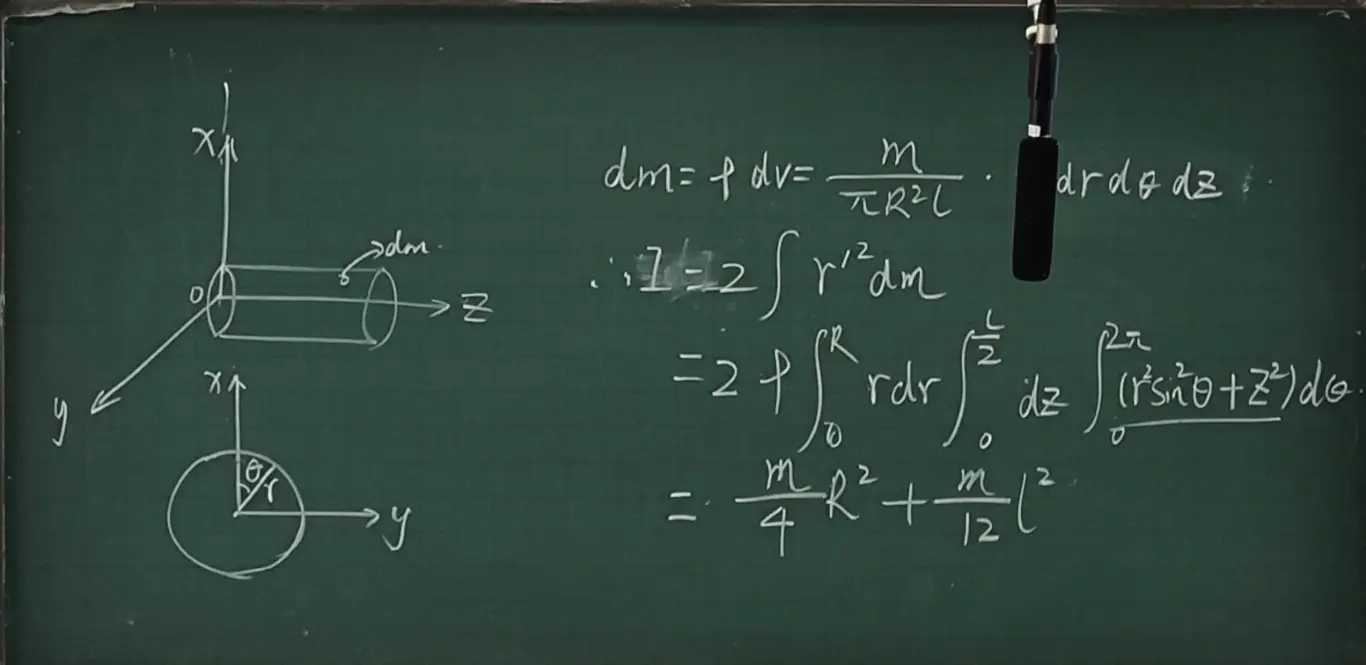物体转动的难易程度
I=∫r2dm
也可以用 J 表示
常见几何物体转动惯量
xoy 细圆环:
I=∫02πR22πRmRdθ=mR2
yoz 细圆环:
根据 xoy 细圆环的转动惯量,在 z 方向上的转动惯量是 mR2
由 垂直轴定理 得:
I=21mR2
xoy 圆薄片:
I=∫02πdθ∫0Rr2πR2mrdr=21mR2
xoy 圆筒:
I=∫02πdθ∫r1r2dr∫0hr2rρdz=2π⋅4(r24−r14)h⋅r22−r12m=2m(r12+r22)
xoy 圆柱:
当 xoy 圆筒内半径趋于 0 的时候,就是圆柱的转动惯量
I=21mr2
xoz 圆柱:
转换为柱坐标 (r,θ,z)
ρ=πr2lm
I=∭(z2+(rsinθ)2)ρdV=∫02πdθ∫0Rrdr∫2l2l(z2+(rsinθ)2)πR2lmdz=πR2lm∫02πdθ∫0Rrdr∫2l2lz2dz+πR2lm∫02πsin2θdθ∫0Rr3dr∫2l2ldz=121ml2+41mr2
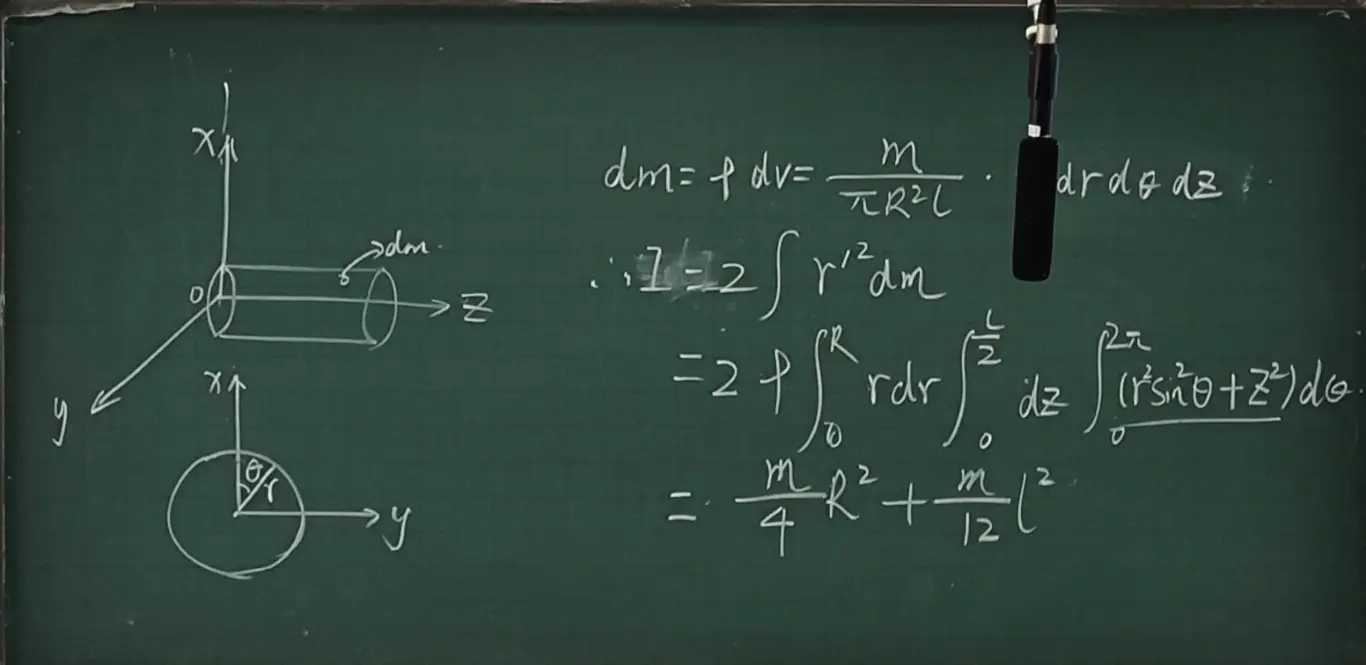
xoz 细棒:
xoz 圆柱当半径 r 趋近于 0 的时候,则为细棒的转动惯量
I=121ml2
如果设 r=2l
I=31mr2
xoz 在一侧的细棒:
如果把另一半补上:
2I=31(2m)r2
根据对称性,一半的转动惯量是一半
I=31mr2=31ml2
这里规定 r=l
球:
I=2π∫0Rdr∫0πr2⋅r2sinφ43πR3mdφ=52mR2
球壳:
设内直径为 R’
I=2π∫R′Rdr∫0πr2⋅r2sinφ43π(R3−R′3)mdφ=52mR3−R′3R5−R′5
取极限 R′→R
I=32mR2
或用轮换对称性作区面积分
I=32∬(x2+y2+z2)ρdS=32r2⋅m