循环码

循环冗余校验

如果一个线性分组码的任意一个码字都是另一个码字的循环移位，称为循环码

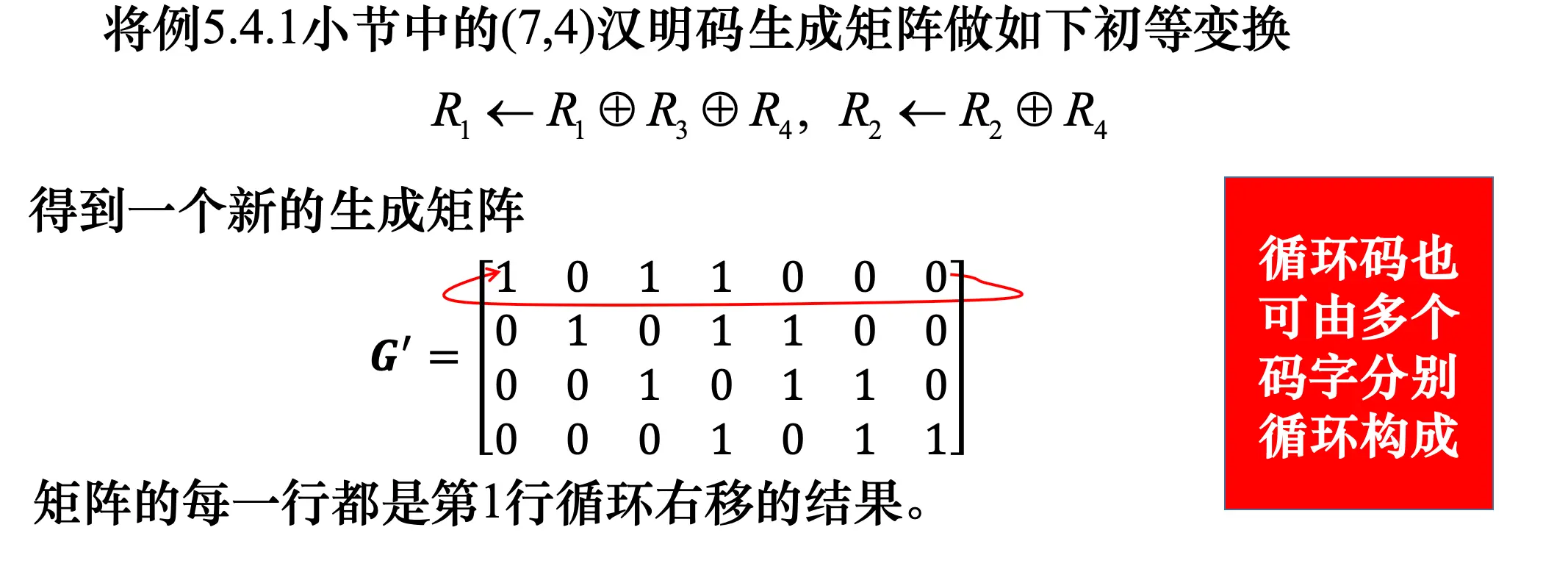
循环码可用多项式描述其循环右移过程（不过系数顺序从右向左书写）

$(n,k)$ 循环码中存在一个非零的，首一的最低次数为 $r(r<n)$ 的码式，满足：

1. $g(x)$ 是唯一的
2. $g(x)$ 的零次项不为零
3. $c(x)$ 是码式当且仅当 $c(x)$ 是 $g(x)$ 的倍式
4. $r=n-k$

则 $g(x)$ 称为循环码的生成多项式，

有定理：

$g(x)$ 为循环码的生成多项式，当且仅当 $g(x)$ 是 $x^n-1$ 的 $r=n-k$ 次因式

• 码字集合是一个 理想，而 $x^n-1$ 是这个理想中的 零元，是一个合法码字，而所有码字都是 $g(x)$ 的倍式，所以 $x^n-1$ 一定是 $g(x)$ 的倍式
• 同时因为 $g(x)$ 是 $x^n-1$ 的因子，所有码字乘以 x 再 $(\mathrm{mod}{x}^{n-1})$ 就是在减去一个 $xg(x)$ 的倍数，其结果也是 $g(x)$ 的倍数，满足了循环性

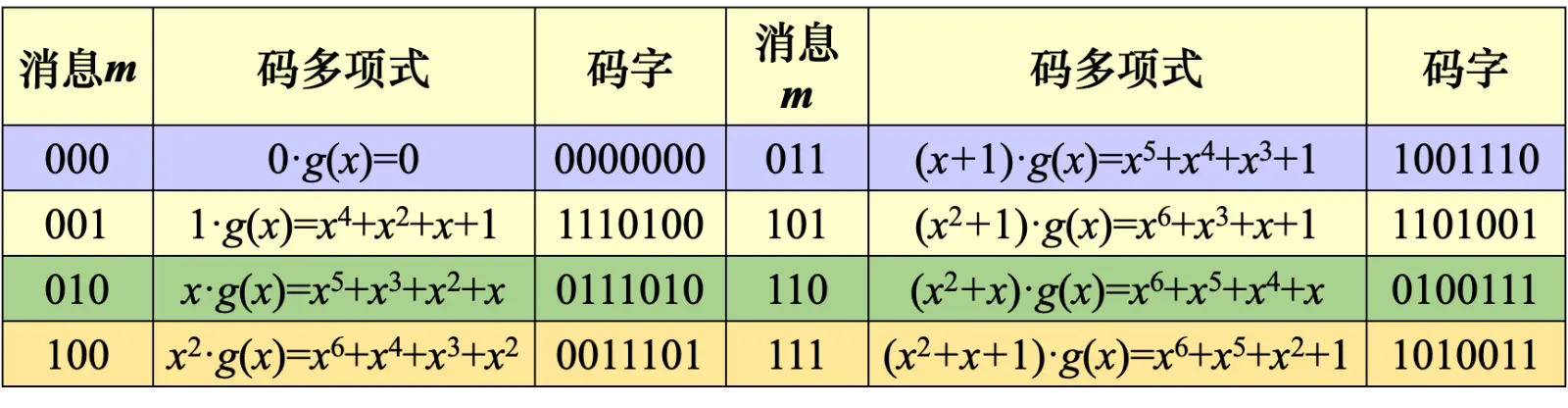
解码需要查这个表转换回去（有点不方便）

校验

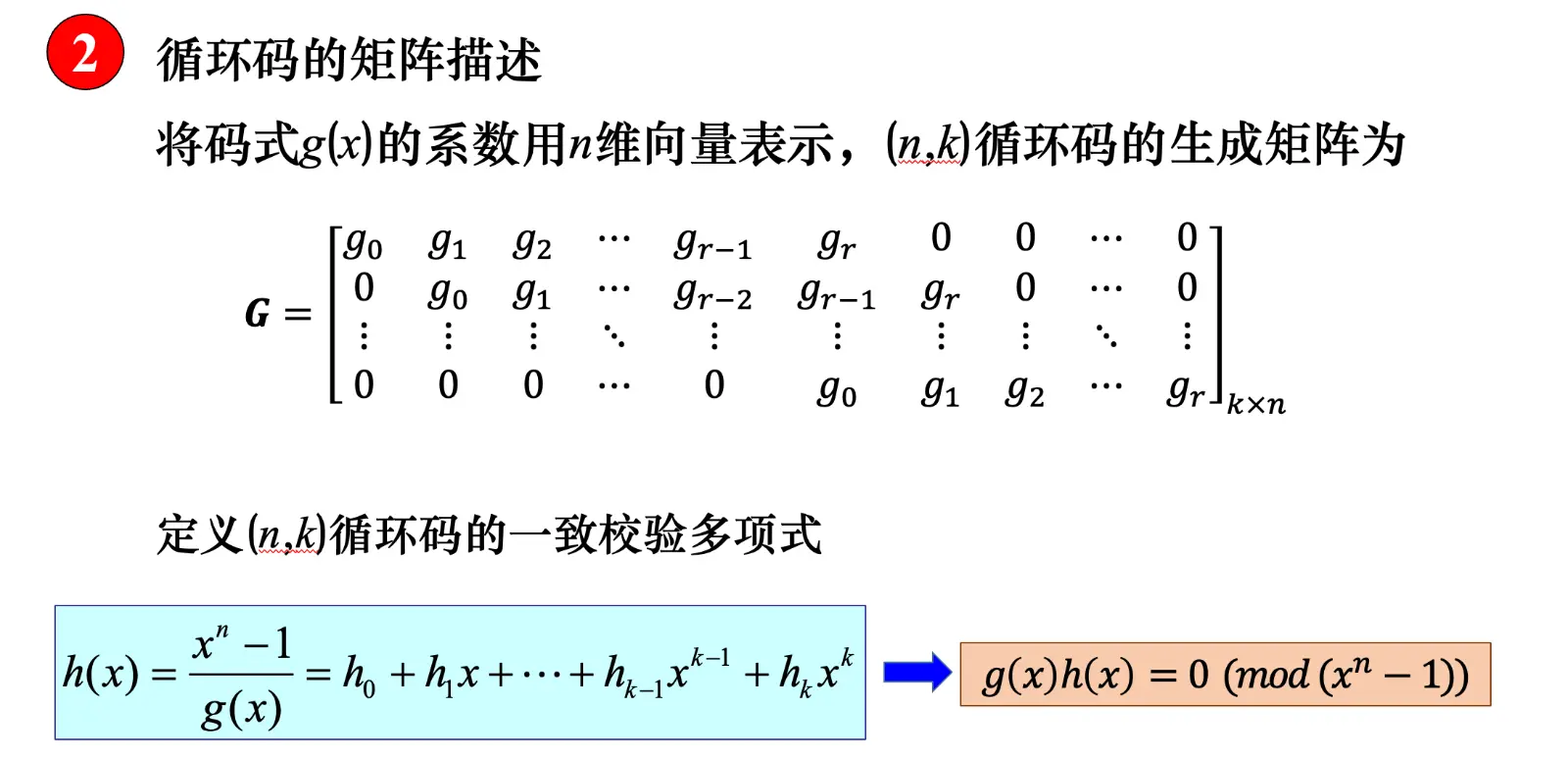
有 $c(x)h(x)=m(x)g(x)h(x)=0(\mathrm{mod}{x}^n-1)$ 校验