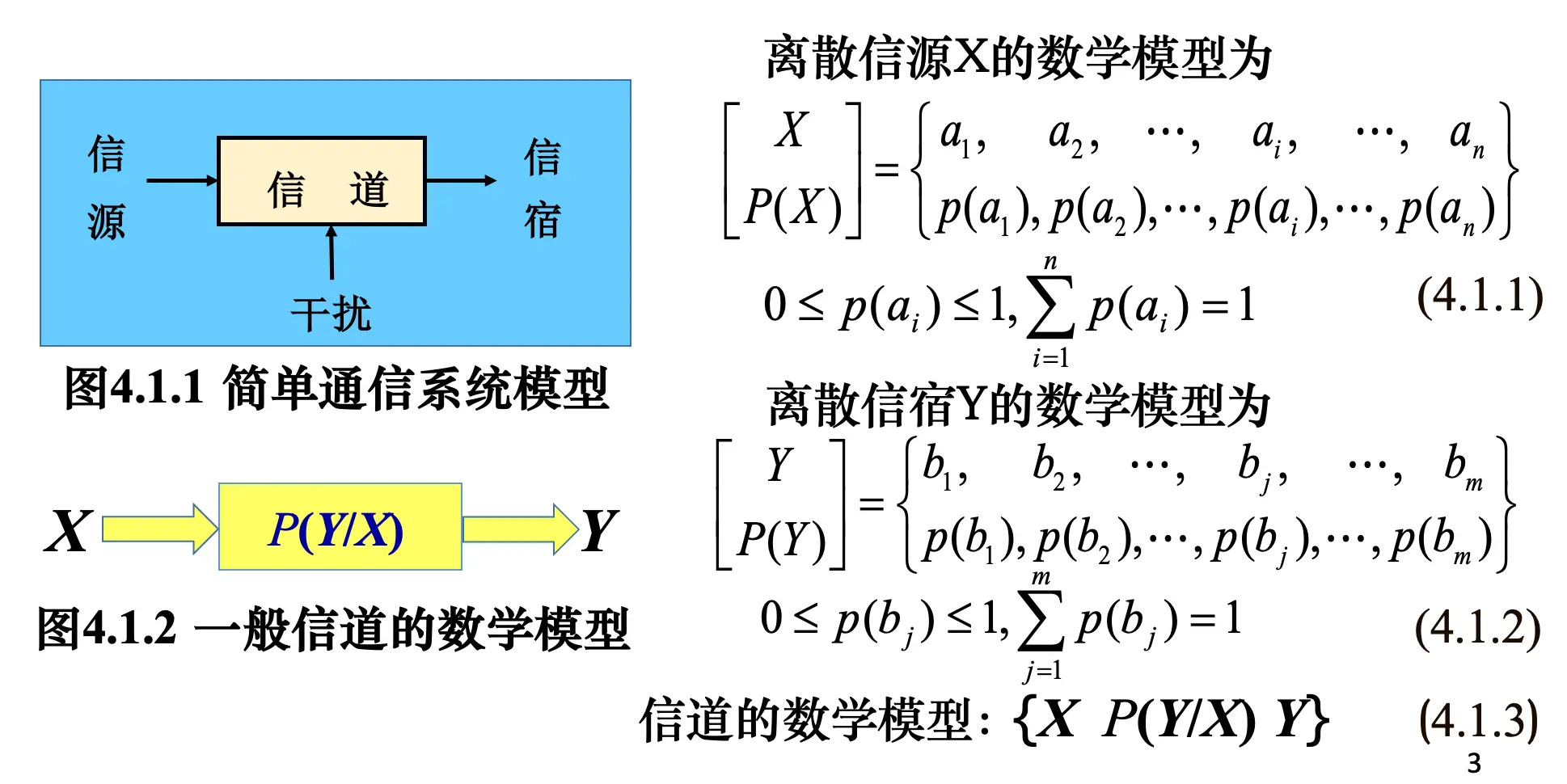
信息度量的方法有很多，这里用的是统计度量

离散信源：信源输出的是一个个符号，符号的取值是可数的，取自一个有限集合

有简化符号：

p (a_{i}) = P (X = a_{i})

p (a_{i} ∣ b_{j}) = P (X = a_{i} ∣ Y = b_{j})

这里的概率实际上就是一个分布，彼此之间不一样

单符号离散信源的数学模型
$[X P (X)] = [a_{1}, a_{2} \dots p (a_{1}), p (a_{2}), \dots]$
大写字母代表随机变量，a 是具体的某个符号

$P$ : 信道转移概率矩阵，维度为 $n \times m$ 。矩阵的第 $i$ 行第 $k$ 列元素 $P_{ik} = p (b_{k} ∣ a_{i})$ 表示输入为 $a_{i}$ 时，输出为 $b_{k}$ 的概率。
$P = p (b_{1} ∣ a_{1}) p (b_{1} ∣ a_{2}) ⋮ p (b_{1} ∣ a_{n}) p (b_{2} ∣ a_{1}) p (b_{2} ∣ a_{2}) ⋮ p (b_{2} ∣ a_{n}) \dots \dots ⋱ \dots p (b_{m} ∣ a_{1}) p (b_{m} ∣ a_{2}) ⋮ p (b_{m} ∣ a_{n})$

注意这里不是直接右乘 X，而是要转置一下。之所以这样做，是为了方便直接定位到“i 行 j 列”

指向原始笔记的链接

满足一系列归一化、正值的性质

自信息量极其性质

自信息量
一个随机事件发生某一个结果后可以得到的信息量
$I (a_{i}) = - lo g p (a_{i})$
概率越小，信息量越大；概率越大，信息量越小；一个确定事件的信息量是 0

可以看作特定事件的“惊喜度”

单位：比特（bit 2）、奈特（nat e）、哈特（hart 10）

自信息量是一个随机变量的函数，可以推广到联合自信息量

当相互独立的时候，对数有一个比较好的性质：
$I (a_{i} b_{i}) = I (a_{i}) + I (b_{i})$
自信息量的定义可通过公理化条件唯一确定。

自信息量的性质

非负性： $I (p) \geq 0$ ;

单调性： $p$ 越小， $I (p)$ 越大;

可加性： $I (p_{1} p_{2} ) = I (p_{1} ) + I (p_{2})$ 。

指向原始笔记的链接

联合自信息量
$I (a_{i} b_{j}) = - lo g p (a_{i} b_{j})$
当 X 和 Y 相互独立的时候，有
$I (a_{i} b_{j}) = I (a_{i}) + I (b_{j})$

我们在用对数衡量世界概率的时候，对于两个独立事件同时发生所带来的信息理解成它们各自带来的信息相加

指向原始笔记的链接

条件自信息量
$I (a_{i} ∣ b_{j}) = - lo g p (a_{i} ∣ b_{j})$ $I (ab) = I (a) + I (b ∣ a) = I (b) + I (a ∣ b)$
即
$I (a ∣ b) = I (ab) - I (b)$

不确定度表示含有多少信息，信息量表示随机事件发生后能够得到多少信息

在已知 b 事件发生之后，如果 a 发生可以得到多少信息，这个信息量可以用 ab 同时发生得到的信息量减去 b 发生得到的信息量得到

表示 b 发生了，a 发生还能多带来的“惊喜度”。（可以假想两个几乎是因果的事件和同时买两种彩票）

指向原始笔记的链接

信源熵及其性质

信源熵
信源熵

各个离散消息自信息量的数学期望，即信源的平均信息量。单位：比特/符号
$H (X) = E (I (X))$

表示信源输出后，离散消息所提供的平均信息量

表示输出前，信源的平均不确定度。不确定度越高（越靠近等概率），熵越高。

反映了变量 X 的随机性

指向原始笔记的链接

条件熵
$H (X ∣ Y) = E (I (a_{i} ∣ b_{i})) = \sum\sum p (a_{i} b_{i}) I (a_{i} ∣ b_{j})$
这里是联合概率 $p (a_{i} b_{i})$ ，因为这里是两个变量的期望（两个自由度），要算两次，一次条件，一次单独的变量，合在一起就是联合概率了

代表在知道 X 的前提下，随机变量 Y 的平均剩余的不确定性。是一个单一的数值，概括了 X 变化时，Y 不确定性的整体情况

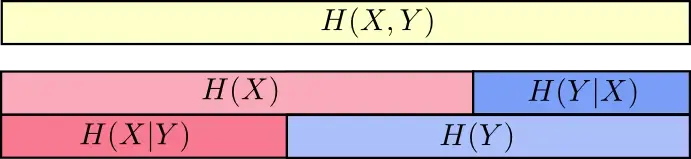
链式法则
$H (Y ∣ X) = H (X, Y) - H (Y)$ 指向原始笔记的链接

联合熵
$H (X Y) = \sum\sum p (ab) I (ab)$
指向原始笔记的链接

信息熵的性质

可加性： $H (X Y) = H (X) + H (Y ∣ X) = H (Y) + H (X ∣ Y)$

非负性：熵结果非负

对称性：熵只和结构有关，不与具体的值有关（变量取值或者顺序）

最大离散熵定理：包含 n 种不同的离散信息，最大的信源熵是 $H (X) = lo g_{2} n$ ，证明：

$H (X) - lo g n = \sum p lo g p^{- 1} - \sum p lo g n = \sum p lo g (\frac{1}{n p})$
令 $x = \frac{1}{n p}$ ，因为 $ln x \leq x - 1$
$\sum p lo g (\frac{1}{n p}) = \sum p \frac{ln ( \frac{1}{n p} )}{ln 2} \leq \frac{1}{ln 2} \sum p (\frac{1}{n p} - 1) = \frac{1 - \sum p}{ln 2} = 0$
等式取等当且仅当 $x = \frac{1}{n p} = 1$ ，所以是等概率时最大

扩展性：当一个事件概率很小的时候，它的信息量很大，但是对整个信息熵的影响很小。 $x ln x \to 0$

确定性：当有一个是 1 的时候（确知信源），最后的熵的结果为 0

极值性：对任意两个消息数相同的信源，有：

$H [p (a_{1}), p (a_{2}) \dots] \leq - \sum p (a_{i}) lo g p (b_{i})$
对其他信源的自信息量与自身分布求期望，结果要大于自身的熵。这个可以推出：
$H (X ∣ Y) \leq H (X)$

即已知 Y 的信息会导致 X 的不确定度下降

上凸性：熵是一个严格上凸函数： $H (α P + (1 - α) Q) > α H (P) + (1 - α) H (Q)$

指向原始笔记的链接

冗余度、自然语信源及信息变差

🪴 Cyril

探索

离散信息源

单符号离散信源的数学模型

自信息量极其性质

自信息量

自信息量的性质

联合自信息量

条件自信息量

信源熵及其性质

信源熵

信源熵

条件熵

链式法则

联合熵

信息熵的性质

关系图谱

目录

最近笔记

信源熵

学习方法论

反向链接