在平面上的情况
原函数是否存在?
如何把原函数算出来?
定积分本质上是 第二类曲线积分,所以如果 u 存在,则要采用第二类曲线积分来运算
定理
D 为单连通偏导连续区域,全微分的原函数存在,等价于 (在 D 内)
证明方式和 曲线积分与路径的无关性 差不多
计算
充分利用路径无关性,写成两个折线:
先横
先竖
如果左端表达式刚好有原函数,则称为 全微分方程
则
为全微分方程的解,算出来是一个一元隐函数的方程形式
第二类曲线积分法
把路径设置一个原点作为途经点,然后扔掉起点到原点的路径(常数),也就是等于原点到终点的任意路径积分即可
Warning
这里千万不能漏掉积分上下限写成不定积分,否则结果会发生改变
凑微分方法

偏积分法
如果验证了原函数存在,那么
再求导解得
空间曲线的情况
在 曲面的单连通区域 上,函数分量有一阶连续偏导数,那么第二类曲线积分与路径无关的等价条件:
由 曲线积分与路径的无关性 等价条件传递性可知
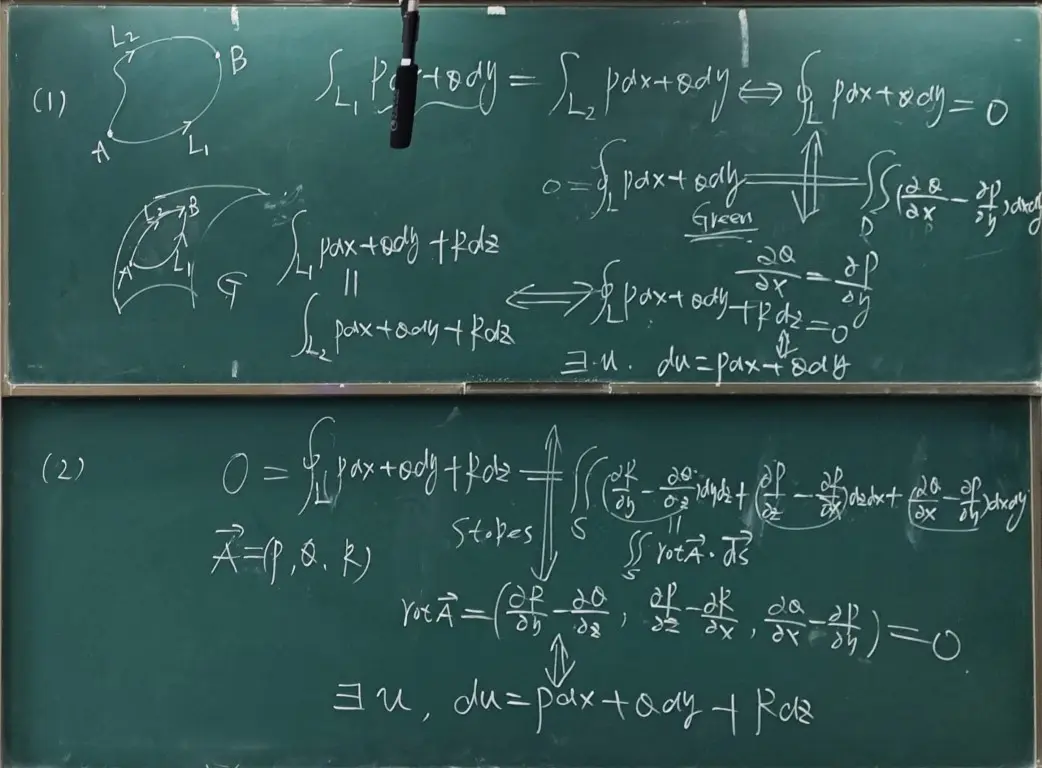
计算积分方法和上面类似