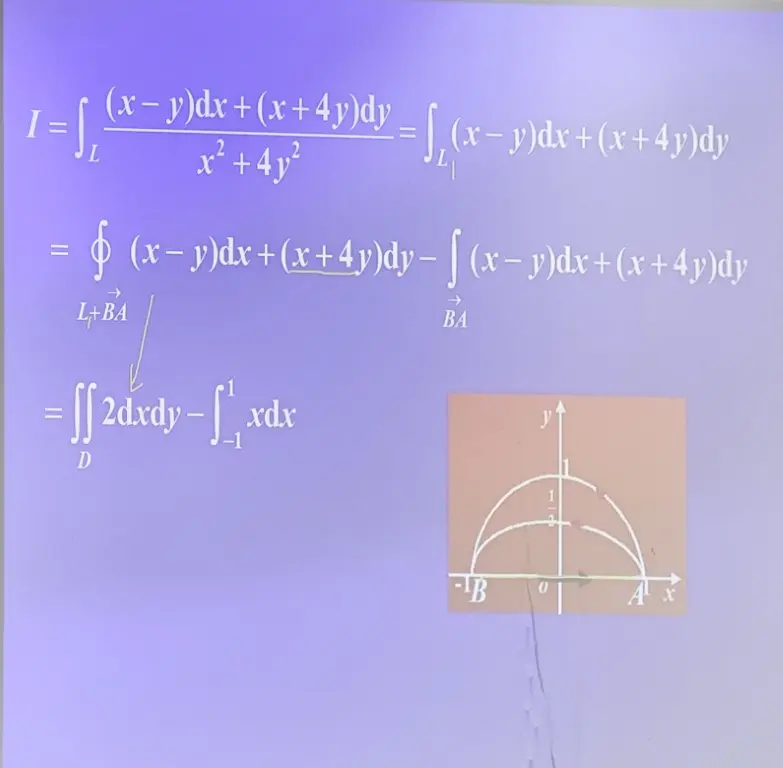曲线积分与路径的无关性

区域 D 内向量场一阶偏导连续

如果 D 内任意两个指定点 AB 以及在 D 内从 A 到 B 两点的任意两条曲线上的 第二类曲线积分 相等，则称 第二类曲线积分 在 D 内与路径无关

点是任意的，路径是任意的

---

判据

1. （充要条件）沿任意封闭曲线的积分等于 0

2. （充要条件）$\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$

证明用反证法：

1. 设在某一个点不相等，不妨设作差大于零
2. 因为两个偏导数连续，作差也连续，在某个邻域内，设半径为 $\frac{n}{2}$
3. 一定能够确定在这个区域内作差也大于 $\frac{n}{2}$ 在这个邻域内积分结果就不为 0 了

→ 格林公式

1. 当满足一节偏导连续的区域是 复连通 的时候，如果有 $\frac{\partial P}{\partial y}=\frac{\partial Q}{\partial x}$，则曲线连续变化不影响结果，只要不经过非解析点就行
2. 被积函数是某个函数的全微分

---

题型：

已知积分与路径无关，可以求出被积函数之中的位置参量

已知积分和路径无关，则可以用特殊路径来计算达到简化的目的：

1. 采用在坐标轴上的折线，这样自变量在特定区间上是 0，消去特定项
2. 采用单位圆，转化为极坐标计算
3. 特殊和一般是相对的，根据分母的形式可以化成椭圆更加简单

偏导数作差是常数，可以考虑 格林公式的运用 转化为算面积，注意补全成封闭的