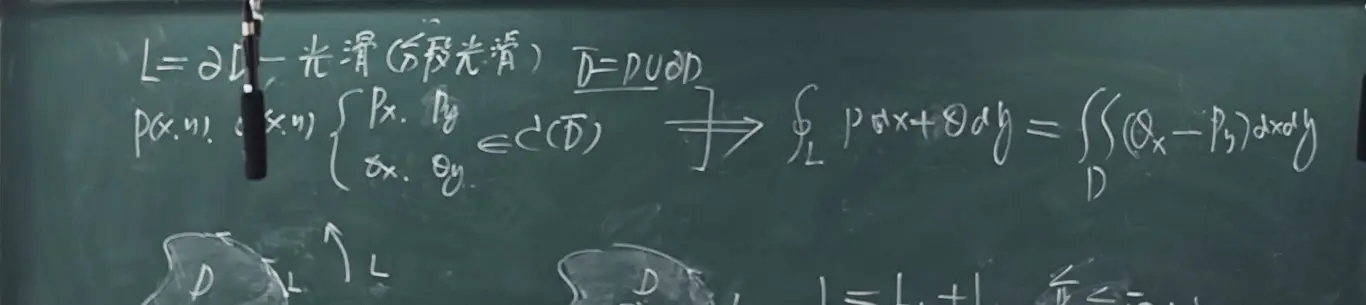区域联通性
曲线L正方向的确定
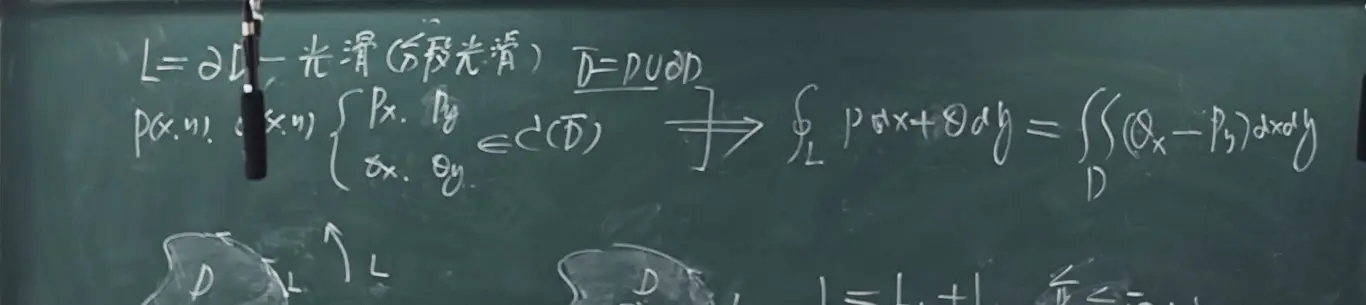
∮LPdx+Qdy=D∬(Qx−Py)dxdy=D∬∂x∂P∂y∂Qdxdy
证明
设区域 D 同时是 x 型 y 型
D∬∂x∂Qdxdy=∫cddy∫x1(y)x2(y)∂x∂Qdx=∫cdQ(x2(y),y)dy−∫cdQ(x1(y),y)dy=∮Q(x,y)dy
用到 第二类曲线积分的计算 逆向思维
另一个同理
−D∬∂y∂Pdxdy=∮P(x,y)dx
相加得到结果
如果不满足 xy 型,用分割可以构造求和,结果一样
如果是 复联通区域,割破连到边界,一样抵消了结果一样
可以推广到有限个洞
若
∂x∂P∂y∂Q=0
则
∮L1+L2Pdx+Qdy=0
∮L1Pdx+Qdy=∮L2−Pdx+Qdy
说明在区域内两个同向的曲线积分是一样的
在单联通上边界取两个异向的曲线
∫C1+C2−Pdx+Qdy=0
∫C1Pdx+Qdy=∫C2Pdx+Qdy
意义:
路径可以往里面变形 →闭路变形原理(收缩的过程要保证偏导数的连续性,至少是存在的吧)
积分和路径无关
格林公式的运用