泊松分布

大量稀有事件发生的次数往往服从泊松分布

$$\underset{n\to \infty }{\lim }B\left(n,\frac{\lambda }{n}\right)$$

大量和稀有是这个模型需要满足的两个条件。可以看 n 很大，p 很小，np 乘积小于 5 即可

对模型进行以下假设：

1. 每做一次实验，发生的次数一定是 1 或者 0
2. 实验之间互相独立

可以想到对时间微分得到近似于这种假设的情况

$$P\{X=k\}=\frac{{\lambda }^k}{k!}{e}^{-\lambda }$$ $$X\sim P(\lambda )$$

---

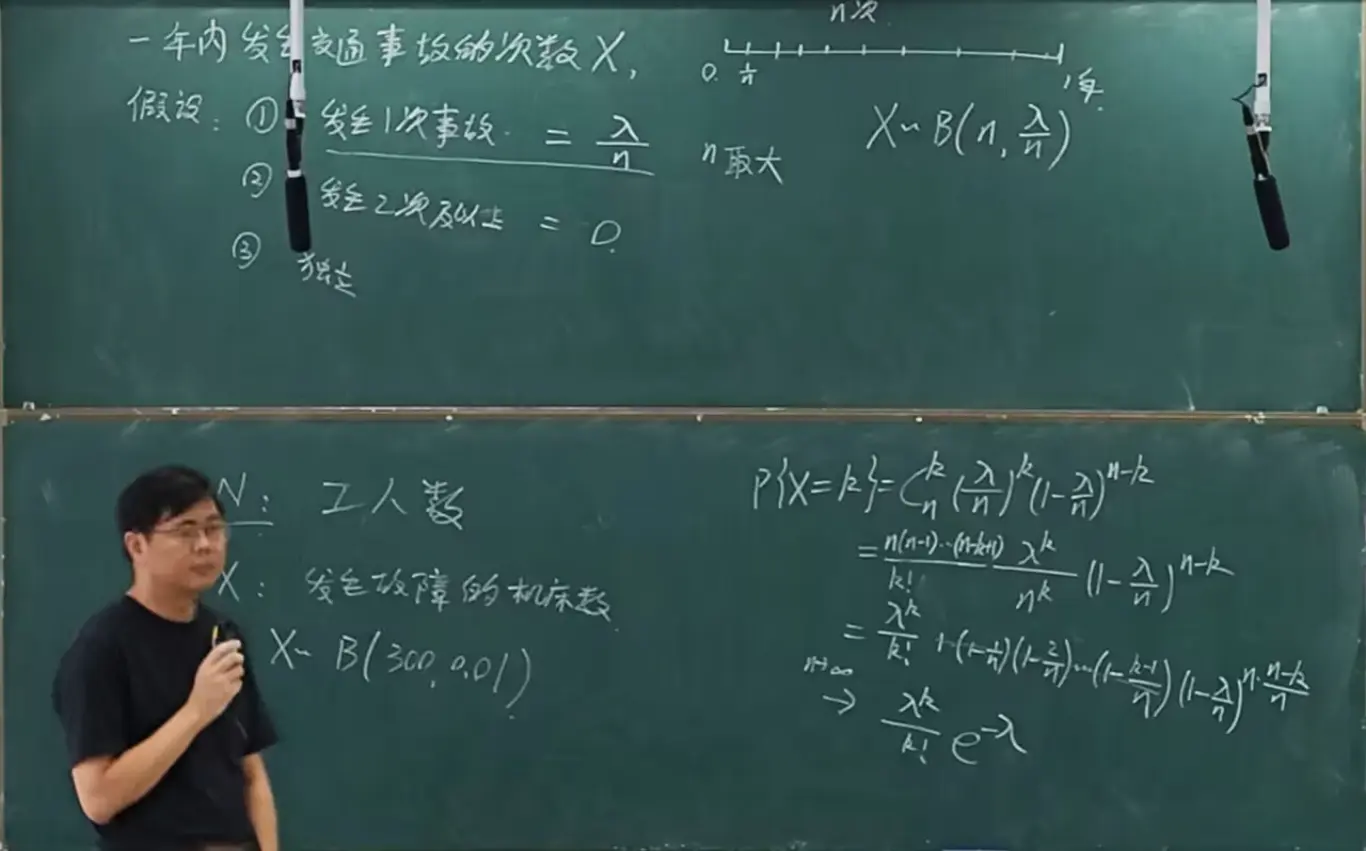
泊松定理

如果二项分布的 n p 有：

$$\underset{n\to \infty }{\lim }n{p}_n=\lambda >0$$

则它的极限就是泊松分布

指向原始笔记的链接

$\lambda$ 称为强度

---

例题：运载火箭中进入仪器仓的宇宙粒子服从参数为 $\lambda$ 的泊松分布，而进入仪器仓的每个粒子落在仪器的重要部位的概率是 p，求恰有 k 个粒子落在仪器重要部位的概率

$$P\{Y=m\}=\frac{{\lambda }^m}{m!}{e}^{-\lambda }$$ $$P\{X=k|Y=m\}=C_m^k{p}^k(1-p{)}^{m-k}$$ $$P\{X=k\}=\sum _{m=k}^{\infty }P\{Y=m\}P\{X=k|Y=m\}=\frac{(\lambda p{)}^k}{k!}{e}^{-\lambda p}$$