高斯公式

空间区域 V 是由分片光滑的闭曲面 S 围成的

$$S=\partial V$$

三个分量函数的 9 个偏导函数在曲面内部连续

则一定有

$$\underset{S}{\iint }Pdydz+\dots =\underset{V}{\iiint }\left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right)dV$$

S 是闭合曲面（打不出来闭合曲面积分符号了）

$$=\underset{S}{\iint }(P\cos \alpha +Q\cos \beta +R\cos \gamma )dS$$

把 单联通区域 和 复联通区域 的概念拓展到空间中，外侧 和 内侧 的概念也拓展

证明思路也和 格林公式 一样，把每一项分别证明再相加即可：

1. V 投影到 xoy 面上，做柱面相切于 V 产生一个切线曲线，分成上下两部分，上部分取上侧，下部分取下侧 $S=S_1+S_2$ $S_1:z=z_1(x,y)$
2. 计算三重积分，运用 第二类曲面积分 的逆方法转换回去：

$$\begin{array}{rl}\iiint \frac{\partial R}{\partial z}dV& =\iint dxdy{\int }_{z_1(x,y)}^{z_2(x,y)}\frac{\partial R}{\partial z}dz\\ & =\underset{D}{\iint }R(x,y,z_2(x,y))-R(x,y,z_1(x,y))dxdy\\ & =\underset{D}{\iint }R(x,y,z_2(x,y))dxdy-\underset{D}{\iint }R(x,y,z_1(x,y))dxdy\\ & \\ & ={\iint }_{S_1}\left(\begin{array}{c}0\\ 0\\ R\end{array}\right)d\vec{S}+{\iint }_{S_2^{-}}\left(\begin{array}{c}0\\ 0\\ R\end{array}\right)d\vec{S}\\ & =\underset{S}{\iint }Rdxdy\end{array}$$

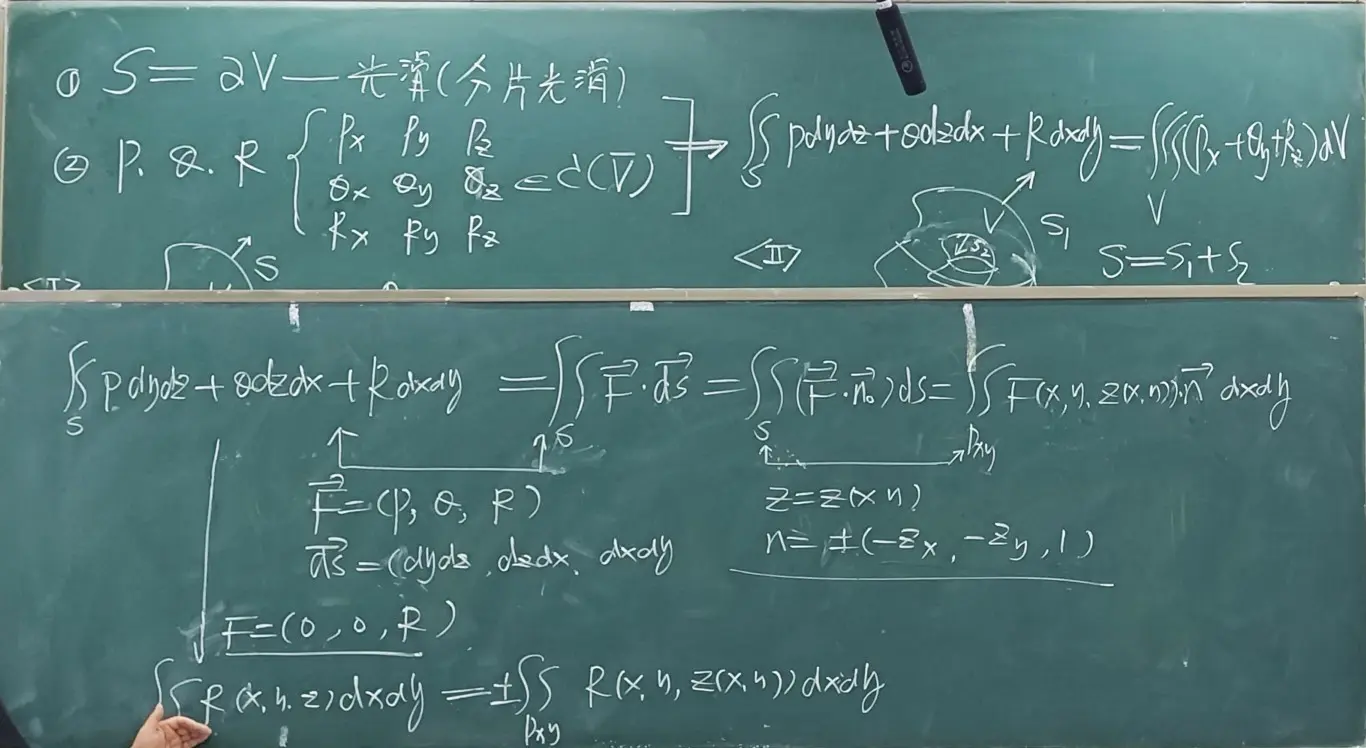
同样可以用这个计算体积，构造右边求导为 1 就行了

---

若

$$P_x+Q_y+R_z=0$$

根据高斯公式，可以得到：

1. 曲面分成两个，互为负项
2. 曲面有内外两个，外面单个曲面向内收缩成里面曲面的结果一样（两个曲面取向一致），里面的可以看成外面的连续收缩，只要不经过偏导数不连续的点就行。可以帮助转化成规则边界的曲面来积分。

---

若记号：

$$\vec{F}=(P,Q,R)$$ $$\nabla \cdot \vec{F}=\frac{\partial P}{\partial x}+\dots$$

散度算子

高斯公式的运用